Оцените значение выражения: 8) номер
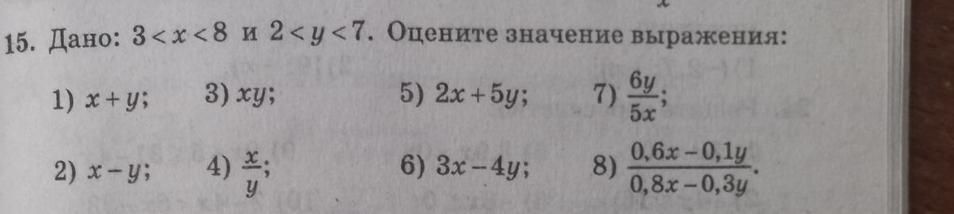
Ответы
Ответ:
11/58 < (0,6х - 0,1у)/(0,8х - 0,3у) < 15 1/3.
Объяснение:
Дано:
3 < х < 8,
2 < у < 7.
Оценить: (0,6х - 0,1у)/(0,8х - 0,3у).
Решение:
1. Заменим данную нам дробь равной, умножив числитель и знаменатель дроби на 10:
(6х - у)/(8х - 3у).
2. Оценим числитель дроби.
а) 3 < х < 8
18 < 6х < 48;
б) 2 < у < 7
- 2 > - у > - 7, т.е.
- 7 < - у < - 2;
в) сложим почленно получившиеся неравенства:
18 - 7 < 6х - у < 48 - 2
11 < 6х - у < 46.
3. Оценим знаменатель дроби:
а) 3 < х < 8
24 < 8х < 64;
б) 2 < у < 7
- 6 > - 3у > - 21, т.е.
- 21 < - 3у < - 6;
в) сложим почленно получившиеся неравенства:
24 - 21 < 8х - 3у < 64 - 6
3 < 8х - 3у < 58.
4. По свойствам числовых неравенств
1/58 < 1/(8х - 3у) < 1/3.
5. Оценим значение частного (данной нам дроби):
Умножим почленно неравенства:
11 < 6х - у < 46
1/58 < 1/(8х - 3у) < 1/3
--------------------------------
11/58 < (6х - у)/(8х - 3у) < 15 1/3