Предмет: Алгебра,
автор: mitzuki058
Доказать, что если {  } и {
} и {  } - ограниченные последовательности , то ограничены и последовательности
} - ограниченные последовательности , то ограничены и последовательности
a) {  }
}
b) {  }
}
leprekon882:
Простая задача
так решите пожалуйста
Я подумала это коментарии к другому вопросу
Ответы
Автор ответа:
1
Модуль произведения равен произведению модулей, а модуль суммы меньше или равен суммы модулей, так что всё очевидно
Если
ну конечно очевидно , только , если a <0 и b <0 , то у вас последний модуль меньше отрицательного числа
и в конце ошибка : < = K |a | +M |b |
В смысле а и b? K и M? они неотрицательные по определению ограниченной последовательности...
a и b - произвольные константы , они могут иметь любой знак
Спасибо!
Автор ответа:
1
Ответ:.................................................
Объяснение:
Приложения:
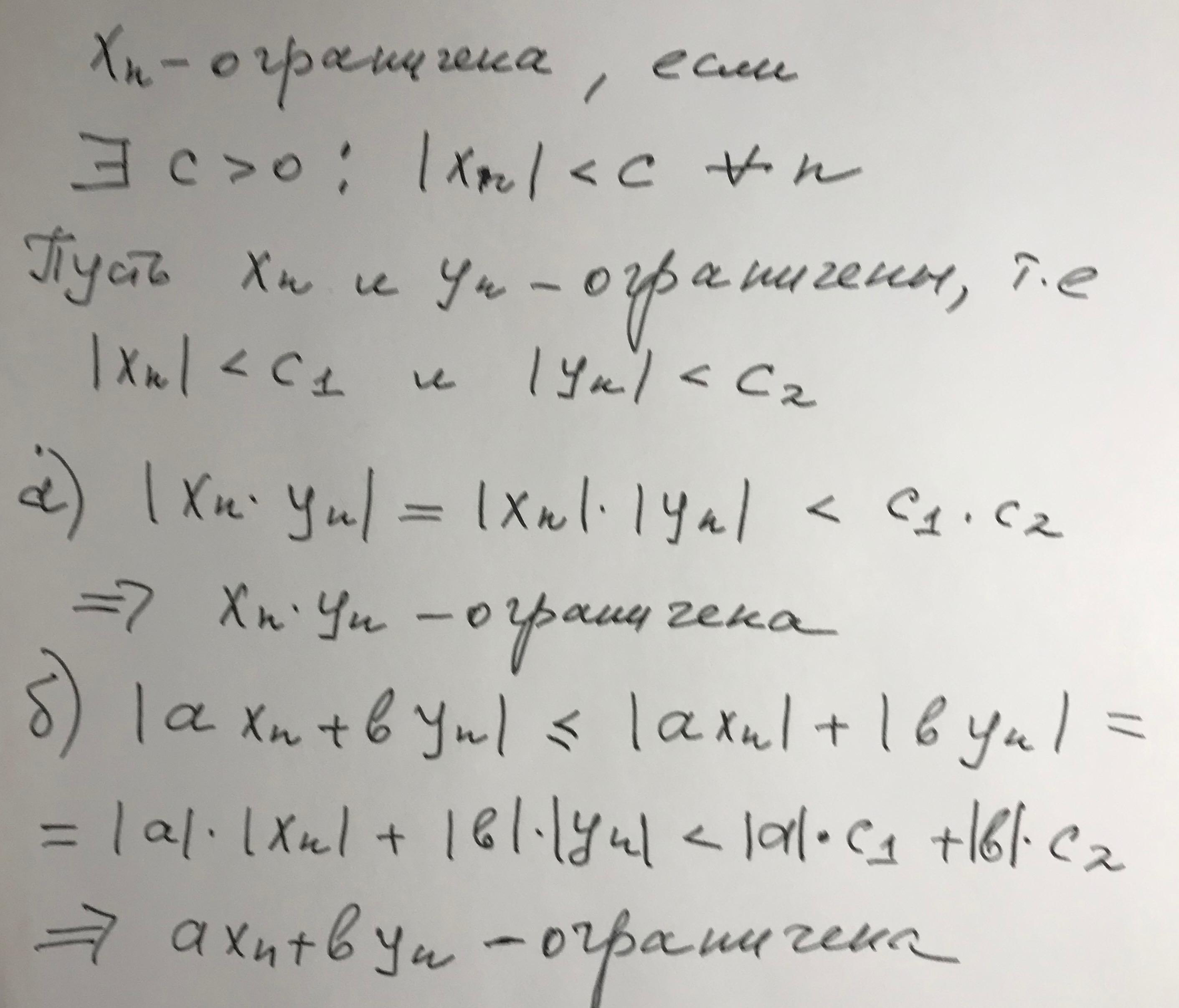
Похожие вопросы
Предмет: Английский язык,
автор: Miiateph
Предмет: История,
автор: gluhovska30
Предмет: Математика,
автор: yure4koi1
Предмет: Алгебра,
автор: melisaoz
Предмет: Обществознание,
автор: shayla0ops