Предмет: Математика,
автор: kakadykakaev
a) Решите неравенство. В ответе укажите произведение наименьшего целого положительного и наибольшего целого отрицательного решений
б) Найдите все значения параметра "а" при каждом из которых неравенство на фото не имеет решений
Приложения:
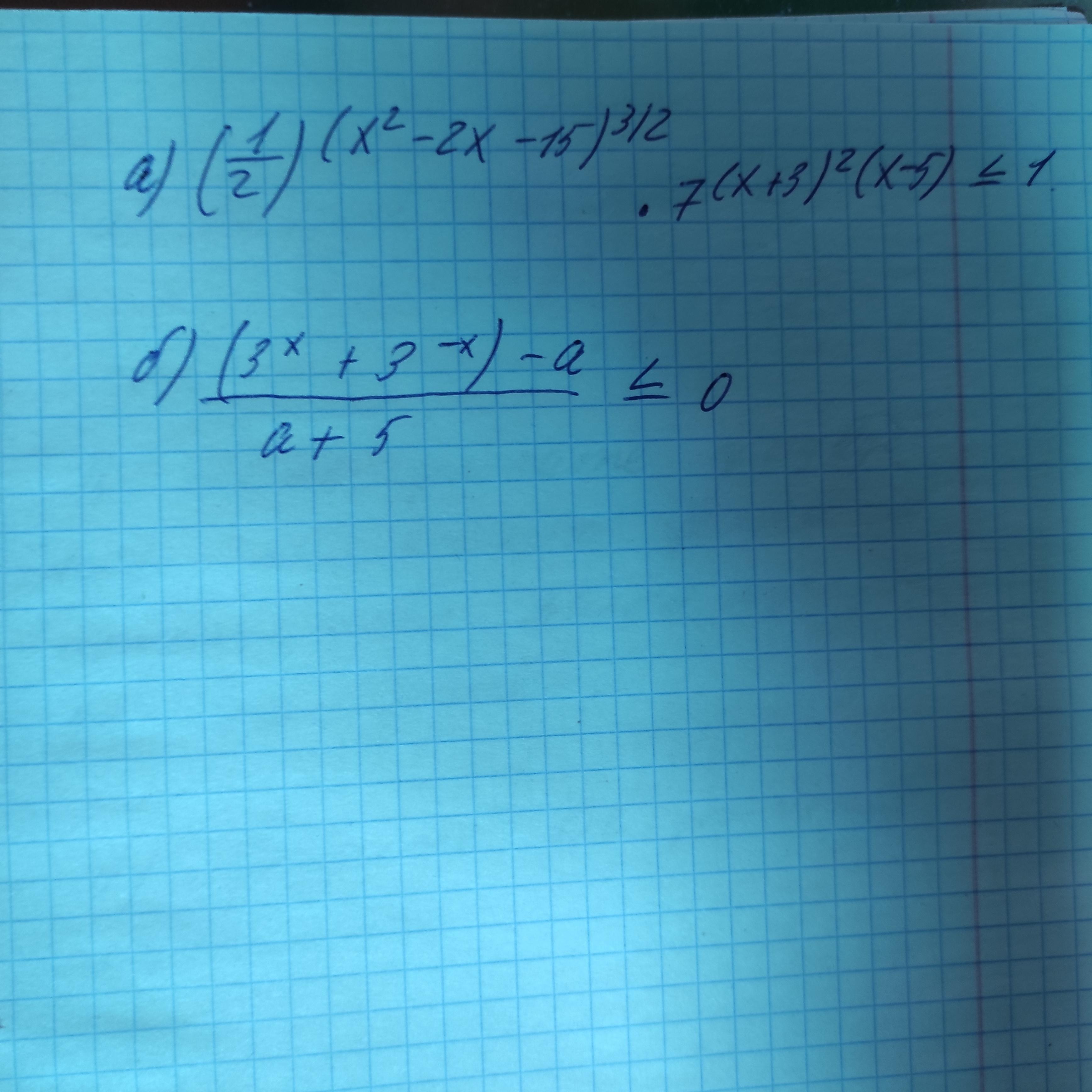
Ответы
Автор ответа:
1
Пошаговое объяснение:
a)
Отсюда следствие, что x≤-3 - решение.
Все выносы за скобки из корня по идее справедливы на этом промежутке, поскольку и (x+3) и (x-5) неотрицательны. Единственный ноль в заданной области(x=5), а при x>5, выражение положительное(подставим, например, x=6), отсюда единственное решение.
Ответ: -15
б)
Сначала разберёмся с :
Следовательно, минимум функции равен 2, достигается при x=0, а область значений данной функции [2;+∞)
Теперь можно сказать, что при -5<a<2 неравенство не имеет решений
Ответ: -5<a<2
На заданной области первое число равно или меньше единицы, другое равно или больше единицы.
Спасибо, УмнейшийКот( или Лис).
Как вам удобнее
Похожие вопросы
Предмет: Математика,
автор: yure4koi1
Предмет: Литература,
автор: alinanovikova0404201
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Raminaleman
"Отсюда следствие, что x≤-3 - решение"