Предмет: Алгебра,
автор: ВладимирБ
Решите уравнение......
Приложения:
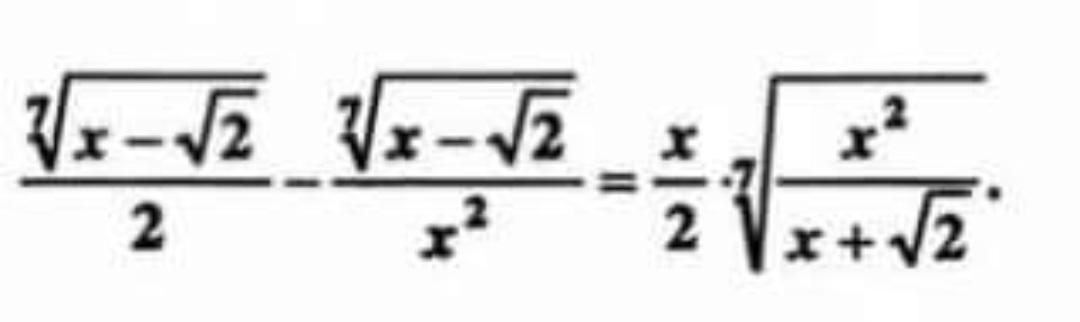
Ответы
Автор ответа:
1
Достаточно заметить, что помимо ОДЗ тут так же не является корнем уравнения, а значит мы можем всё поделить на числитель первых двух дробей
Идея состоит в том, что числитель первых дробей говорят нам, что можно вынести их и дальше оценивать то, что получится во втором множители. Но никакая замена не поможет. Даже если мы заменим числитель первый дробей, то что делать с ? Возводить новую переменную в квадрат и выражать? Нет... Так станет только хуже
По этому я и предлагаю поделить всё на
Тут ничего не остаётся делать, как возводить в седьмую степень, но бояться этого не стоит, знаменатель равен левой части, а значит на него можно домножить
И получается, что уравнение имеет единственное решение
Похожие вопросы
Предмет: Українська література,
автор: zaharcevagalina0
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: Georg981
Предмет: Алгебра,
автор: melisaoz
Предмет: Химия,
автор: dsnilaspakovskij04