Решите уравнение......
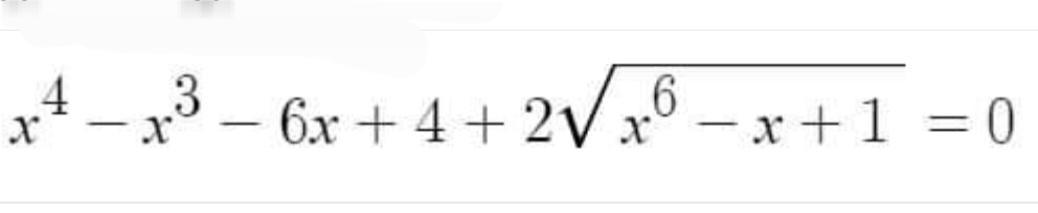
Ответы
Никак тут данное задание не решить иначе, сколько бы я методов не перепробовал. Нужно возводить в квадрат
Заметим, что сумма коэффициентов равна нулю, а значит первый корень - это следствие из теоремы Виета
И снова замечаем, что сумма коэффициентов равна 0, а значит и второй корень
Мы получили уравнение шестой степень, которое не имеет рациональных или целых корней. Корни данного уравнения можно выразить через гипергеометрические функции, но кажется, не такой подход нужен
Заметим, что вещественные и комплексные корни не могут быть заданы в замкнутом виде, то есть в явной форме выражены, поскольку группа Галуа - ...
Уравнение имеет одно решение , но чтобы доказать, что корни уравнения шестой степень не являются корнями первоначального уравнения, нужно численными методами находить корни и подставлять в уравнение, что не есть задумка подобных уравнений
В уравнении явно какая-то ошибка и не учли коэффициенты, так как хороший корень и так должно быть дальше, тогда бы и метод нашёлся, но с нынешними корнями всё плохо...