Question

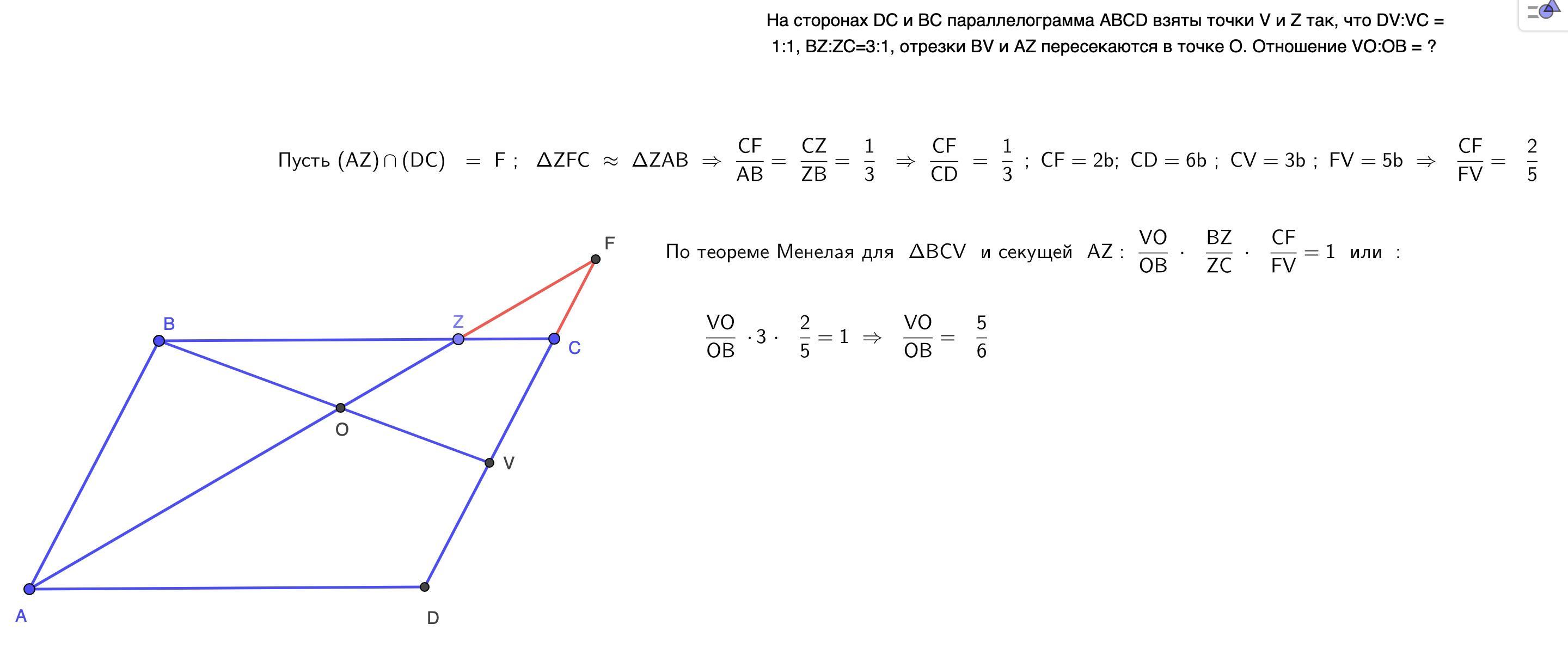
На сторонах DC и ВС параллелограмма ABCD взяты точки V и Z так, что DV:VC = 1:1, BZ:ZC=3:1, отрезки BV и AZ пересекаются в точке О. Отношение VO:OB равно....
5:4
4:5
6:7
1:1
5:6
СРОЧНО!!!!!

Answer 1

Ответ:

Отношение VO : OB равно 5 : 6.

Объяснение:

На сторонах DC и ВС параллелограмма ABCD взяты точки V и Z так, что DV:VC = 1:1, BZ:ZC=3:1, отрезки BV и AZ пересекаются в точке О. Отношение VO:OB равно....

Дано: ABCD - параллелограмм;

V ∈ DC; Z ∈ BC;

DV : VC = 1 : 1, BZ : ZC = 3 : 1,

BV ∩ AZ = O

Найти: VO : OB

Решение:

Проведем VK || BC.

• Теорема Фалеса:
• Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

DV : VC = 1 : 1   ⇒   DV = VC  ⇒   AM = MZ

Пусть ZC = x, тогда BZ = 3x, а KV = 4x.

Рассмотрим ΔABZ.

AM = MZ; KM || BZ

• Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ KM - средняя линия ΔABZ.

• Средняя линия равна половине стороны, которую она не пересекает.

⇒ КМ = BZ : 2 = 3/2 x

Тогда MV = 4x - 3/2 x = 5/2 x

Рассмотрим ΔVOM и ΔBOZ.

• Вертикальные углы равны.

⇒ ∠VOM = ∠BOZ

• При пересечении двух параллельных прямых секущей накрест лежащие углы равны.

⇒ ∠ОVM = ∠OBZ

ΔVOM ~ ΔBOZ (по двум углам)

Запишем отношения сходственных сторон:

$\displaystyle \frac{MV}{ZB}=\frac{VO}{OB}=\frac{5x}{2\cdot3x} =\frac{5}{6}$

Отношение VO : OB равно 5 : 6.

Answer 2

Ответ:

5 : 6 .........................

Объяснение: