Предмет: Математика,
автор: Tokeridze
Подробно с пошаговым решением объяснить решение с теорией
Приложения:
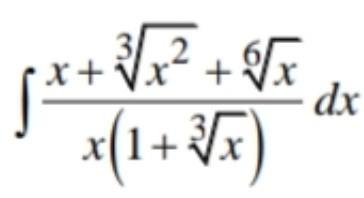
Ответы
Автор ответа:
0
Сделаем замену , тогда наш интеграл равен
Теперь воспользуемся одним трюком
Мы получили табличные интегралы, тогда
Обратная замена
Похожие вопросы
Предмет: География,
автор: darabatozna
Предмет: Другие предметы,
автор: v18269504
Предмет: География,
автор: Gvozdik556773
Предмет: Математика,
автор: darysik12