Предмет: Геометрия,
автор: Bogdanychteren
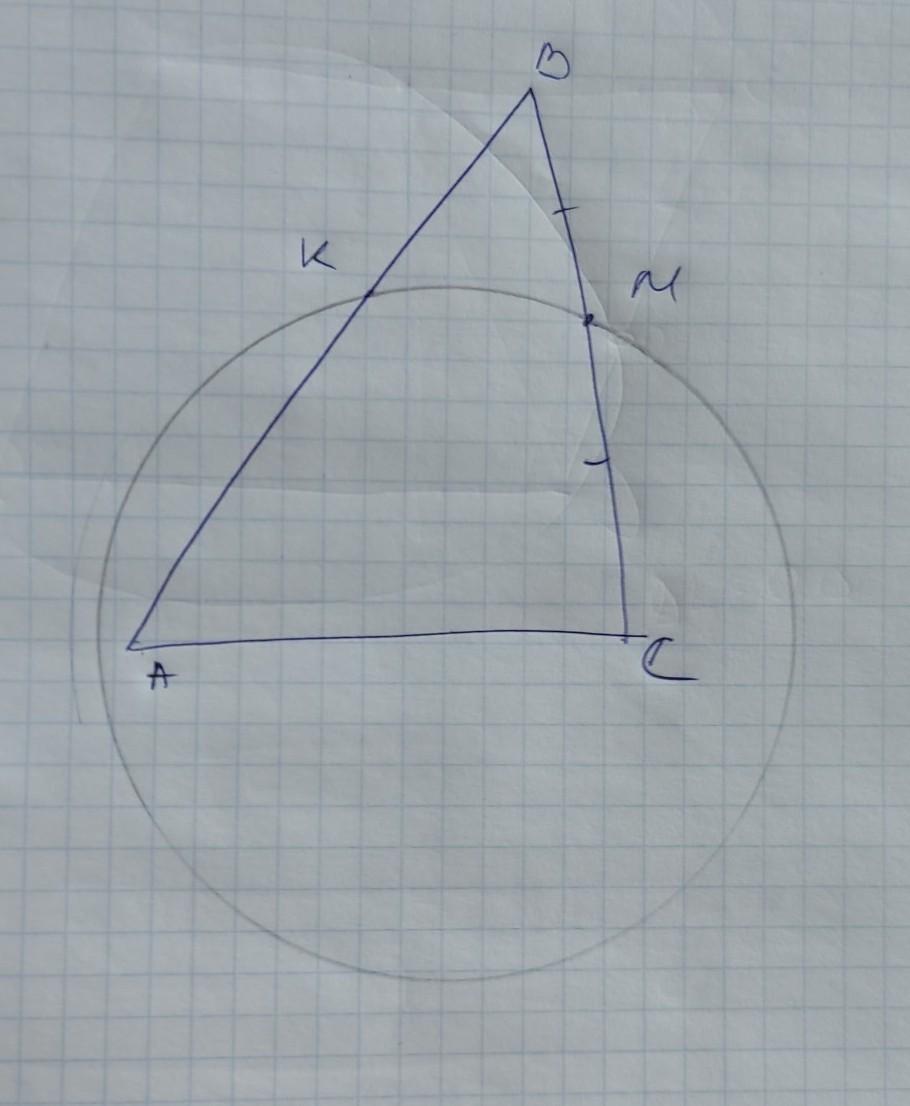
Окружность радиуса R касается сторон АВ и ВС ∆ АВС в точках К и М соответственно. Известно, что центр окружности лежит на стороне АС. М середина ВС, ВК=2АК. Найти площадь треугольника АВС
Приложения:
ГАЗ52:
Чертёж неверный. Кто будет писать решение, сделает.
Ответы
Автор ответа:
2
Ответ:
............................................
Объяснение:
Приложения:
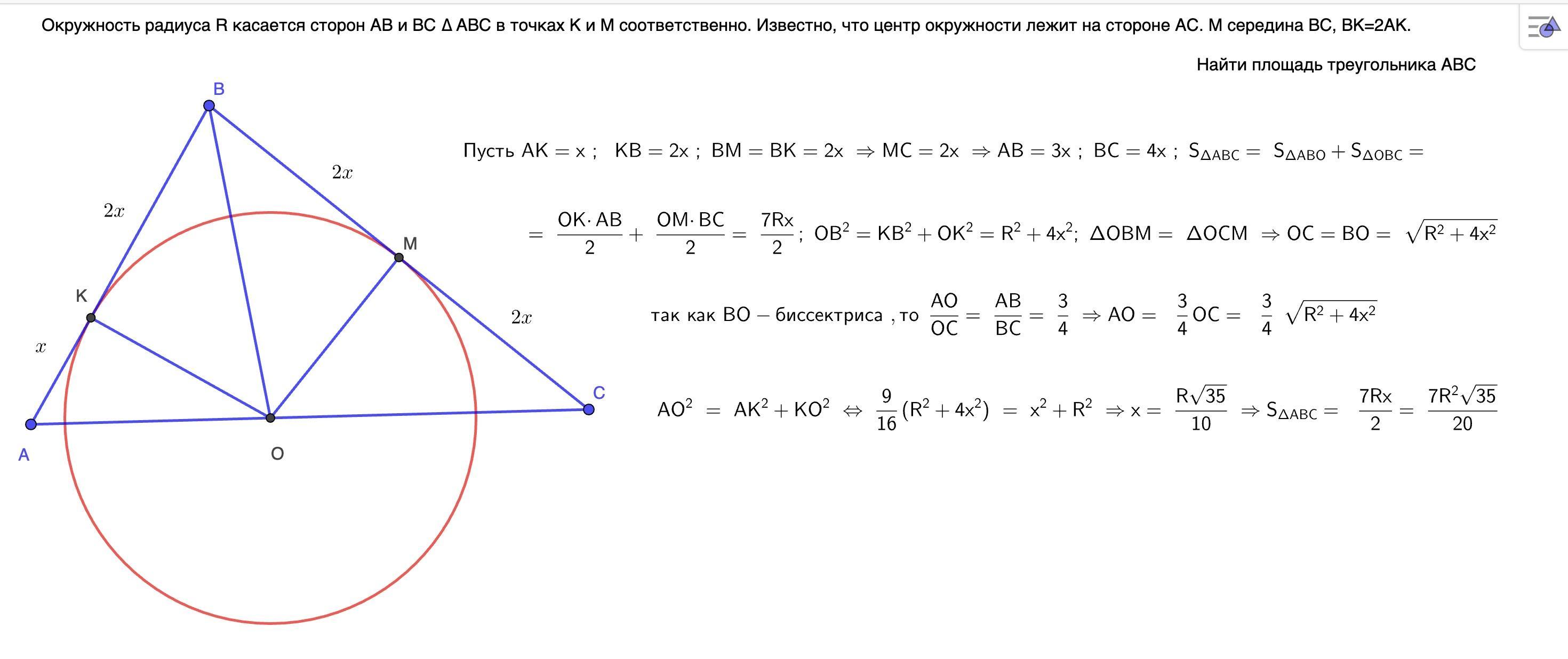
Ответ не очень красивый , но надеюсь верный , может быть Сергей найдёт более простое решение
проще не получилось :)
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Отрезки касательных из одной точки равны, BK=BM
AK=x, BK=BM=2x, AB=3x, BC=4x
Центр вписанной окружности лежит на биссектрисе, BO - биссектриса.
По т о биссектрисе AO/OC=AB/BC =3/4
OM -высота и медиана => △BOC -р/б
AO=3y, OC=BO=4y, AC=7y
△AOB~△ABC => AB/AC=AO/AB => 3x/7y =3y/3x => y/x =√3/√7
OC/MC =4y/2x =2√3/√7
Пусть OC=2√3, MC=√7
По т Пифагора OM =√(OC^2-MC^2) =√5 =R
S(BOC) =1/2 BC*OM =1/2 *2√7*√5 =√35
S(ABC)/S(BOC) =AC/OC =7/4 => S(ABC)=7/4 √35
Нашли искомую площадь при радиусе √5.
Теперь найдем площадь подобного треугольника при радиусе R.
S(R)/S(√5) =(R/√5)^2 => S(R) =7/4 √35 *R^2/5 =7√35/20 R^2
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: Dashapon11
Предмет: Литература,
автор: anastasiyaBlack
Предмет: Геометрия,
автор: kpopmy
Предмет: Алгебра,
автор: Txjdbo
Предмет: Литература,
автор: romangorohov07