Question

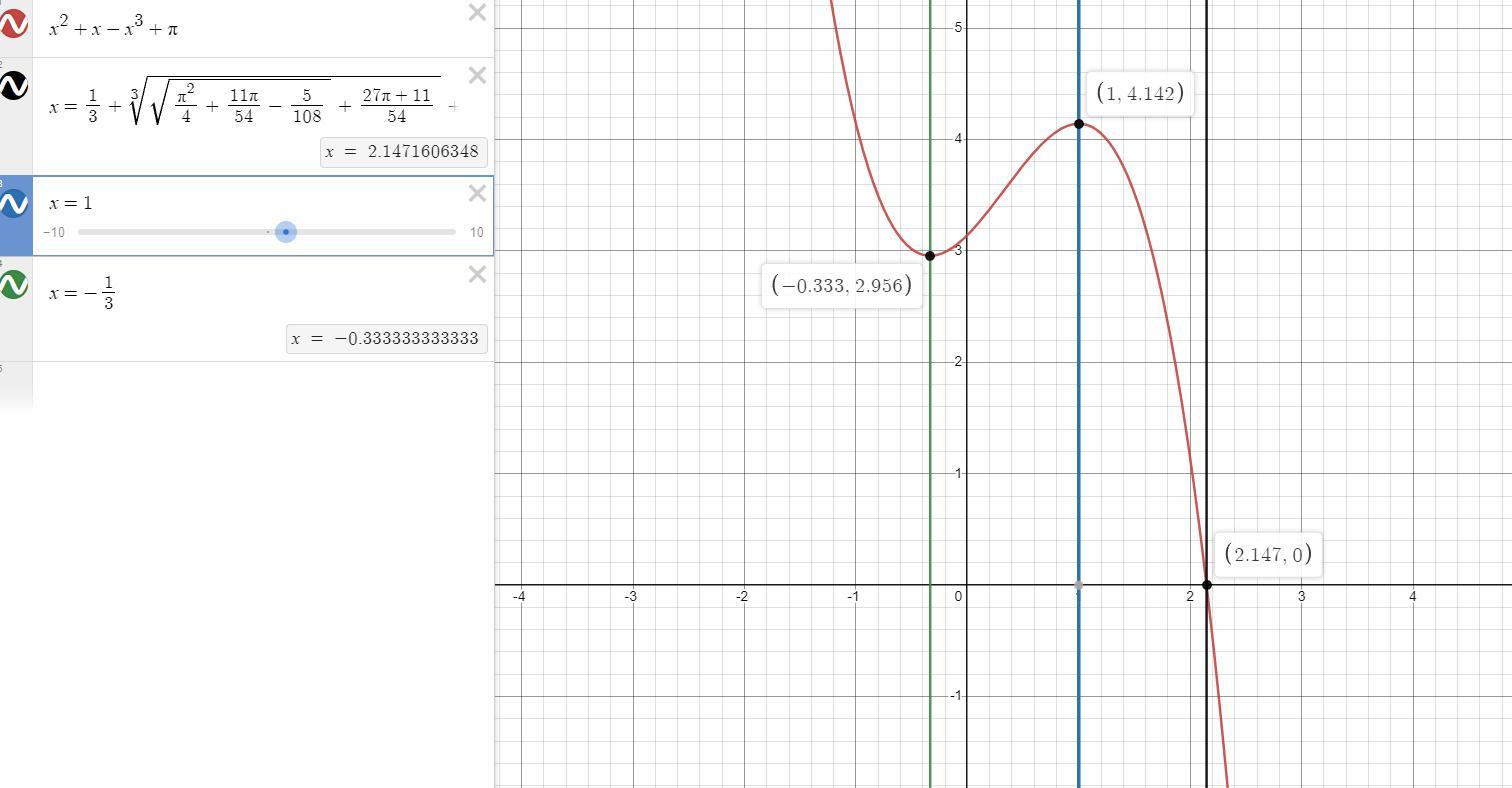
требуется график с исследованиями

y=x^2+x-x^3+π

Answer 1

Стоит сказать, что функция сюръективна на $\mathbb{R}$ и важно заметить, что функция не четная и не нечетная, а общего вида

Точку пересечения в осью Oy находятся довольно просто, достаточно вместо $x$ подставить $0$ и мы получим точку $(0,\pi)$. А вот с Ox пересечение труднее ищется$x^3-x^2-x-\pi=0\overset{x=t+1/3}{\Rightarrow }\left(t+\dfrac{1}{3}\right)^{3}-\left(t+\dfrac{1}{3}\right)^{2}-t-\pi-\dfrac{1}{3}=0\Leftrightarrow \\\Leftrightarrow t^{3}-\dfrac{4\,t}{3}-\dfrac{27\,\pi+11}{27}=0$

Так как $\mathrm{Q}=\left(\dfrac{\mathrm{p}}{3}\right)^3+\left(\dfrac{\mathrm{q}}{2}\right)^2=\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108} > 0$, то кубическое уравнение имеет только один вещественный корень. Найдём его с помощью формулы Кардано

$\mathrm{Q}=\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108},\;\;\mathrm{q}=-\dfrac{27\,\pi+11}{27}\Rightarrow \begin{cases}\alpha=\sqrt[3]{-\dfrac{\mathrm{q}}{2}+\sqrt{\mathrm{Q}}}\\ \beta=\sqrt[3]{-\dfrac{\mathrm{q}}{2}-\sqrt{\mathrm{Q}}}\end{cases}\Rightarrow$$\alpha=\sqrt[{3}]{\sqrt{\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108}}+\dfrac{27\,\pi+11}{54}},\beta=\sqrt[{3}]{\dfrac{27\,\pi+11}{54}-\sqrt{\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108}}}$

$\Rightarrow t=\alpha+\beta=t=\sqrt[{3}]{\sqrt{\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108}}+\dfrac{27\,\pi+11}{54}}+\sqrt[{3}]{\dfrac{27\,\pi+11}{54}-\sqrt{\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108}}}$Обратная замена$x=\sqrt[{3}]{\sqrt{\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108}}+\dfrac{27\,\pi+11}{54}}+\sqrt[{3}]{\dfrac{27\,\pi+11}{54}-\sqrt{\dfrac{\pi^{2}}{4}+\dfrac{11\,\pi}{54}-\dfrac{5}{108}}}+\dfrac{1}{3}$

Теперь найдём интервалы убывания и возрастания$y'=-3x^2+2x+1\\y'=0\Rightarrow -3x^2+2x+1=0\Rightarrow x=\left \{ -\frac{1}{3},1 \right \}$На интервале$\left ( -\infty ,-\frac{1}{3} \right )$ функция убывает. На интервале $\left ( -\frac{1}{3},1 \right )$ функция возрастает. На интервале$\left ( 1,+\infty \right )$ функция убывает. Так как функция меняет знак на каждом интервале, то $x=-\frac{1}{3}$ - точка минимума, а $x=1$ - точка максимума

Найдём нули второй производной, чтобы найти интервалы выпуклости и вогнутости. $y''=2-6x$, $\; y''=0\Rightarrow 2-6x=0\Rightarrow x=\frac{1}{3}$. На интервале $\left ( -\infty ,\frac{1}{3} \right )$ вогнута, а на и $\left ( \frac{1}{3},+\infty \right )$ выпукла Очевидно, что у данной кубической параболы отсутствуют наклонные и горизонтальные асимптоты

Прилепляю фото для проверки корней и самого графика