Question

ПОМОГИТЕ ПОЖАЛУЙСТА
нужно вычислить двойной интеграл

Answer 1

Ответ:

Двойной интеграл:

$\boldsymbol{\boxed{\iint\limits_D {x} \, dxdy = \frac{7}{15}}}$

Пошаговое объяснение:

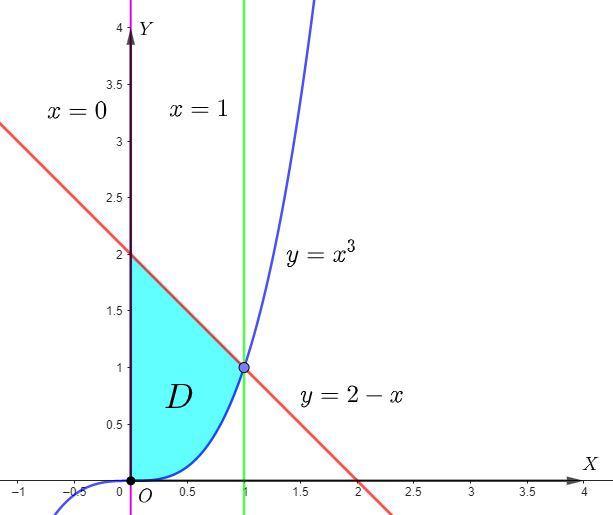
Область $D:$

$y = x^3$

$y + x = 2 \Longleftrightarrow y = 2- x$

$x = 0$

Абсцисса пересечения кривых $y = x^3$ и $y = 2- x:$

$x^3 = 2 - x$

$x^3 + x - 2 = 0$

Делители свободного члена:

$\pm 1,\pm 2$

$x = 1:$

$1^{3} + 1 - 2 = 2-2=0$, то есть $x = 1$ - корень

Вычисление двойного интеграла:

$\displaystyle \iint\limits_D {x} \, dxdy = \int\limits^1_0 dx \int\limits_{x^{3}}^{2-x} {x} \, dy = \int\limits^1_0 {x} \, dx \int\limits_{x^{3}}^{2-x} \, dy = \int\limits^1_0 {x \cdot y \bigg |_{x^{3}}^{2-x} } \, dx =$

$\displaystyle = \int\limits^1_0 {x(2-x-x^{3})} \, dx = \int\limits^1_0 {(2x -x^{2} - x^{4})} \, dx = \bigg(x^{2} - \frac{x^{3}}{3} - \frac{x^{5}}{5} \bigg) \bigg |_{0}^{1} =$

$\displaystyle = \bigg(1^{2} - \frac{1^{3}}{3} - \frac{1^{5}}{5} \bigg) - \bigg(0^{2} - \frac{0^{3}}{3} - \frac{0^{5}}{5} \bigg) = 1 - \frac{1}{3} - \frac{1}{5} = \frac{15 - 5-3}{15} = \frac{7}{15}$