Предмет: Алгебра,
автор: sw3toff
Розв’язати однорідне диференціальне рівняння
Приложения:
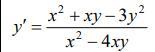
Ответы
Автор ответа:
1
Умножим всё на и сделаем замену
, тогда
, а
, получаем
sw3toff:
Тут не правильное уравнение
Или я ошибаюсь
Почему?
У меня начинается начало уравнения с x^2, а у вас с -3y^2
А, понял, а я думал, что от перестановки слагаемых сумма не меняется
Переделаете?
Вы и правда не понимаете?
2+3 или 3+2 есть разница?
Похожие вопросы
Предмет: Українська мова,
автор: fashiongame111
Предмет: Українська мова,
автор: dumpisner
Предмет: Математика,
автор: lytaivika23
Предмет: Химия,
автор: 7AMG77