Question

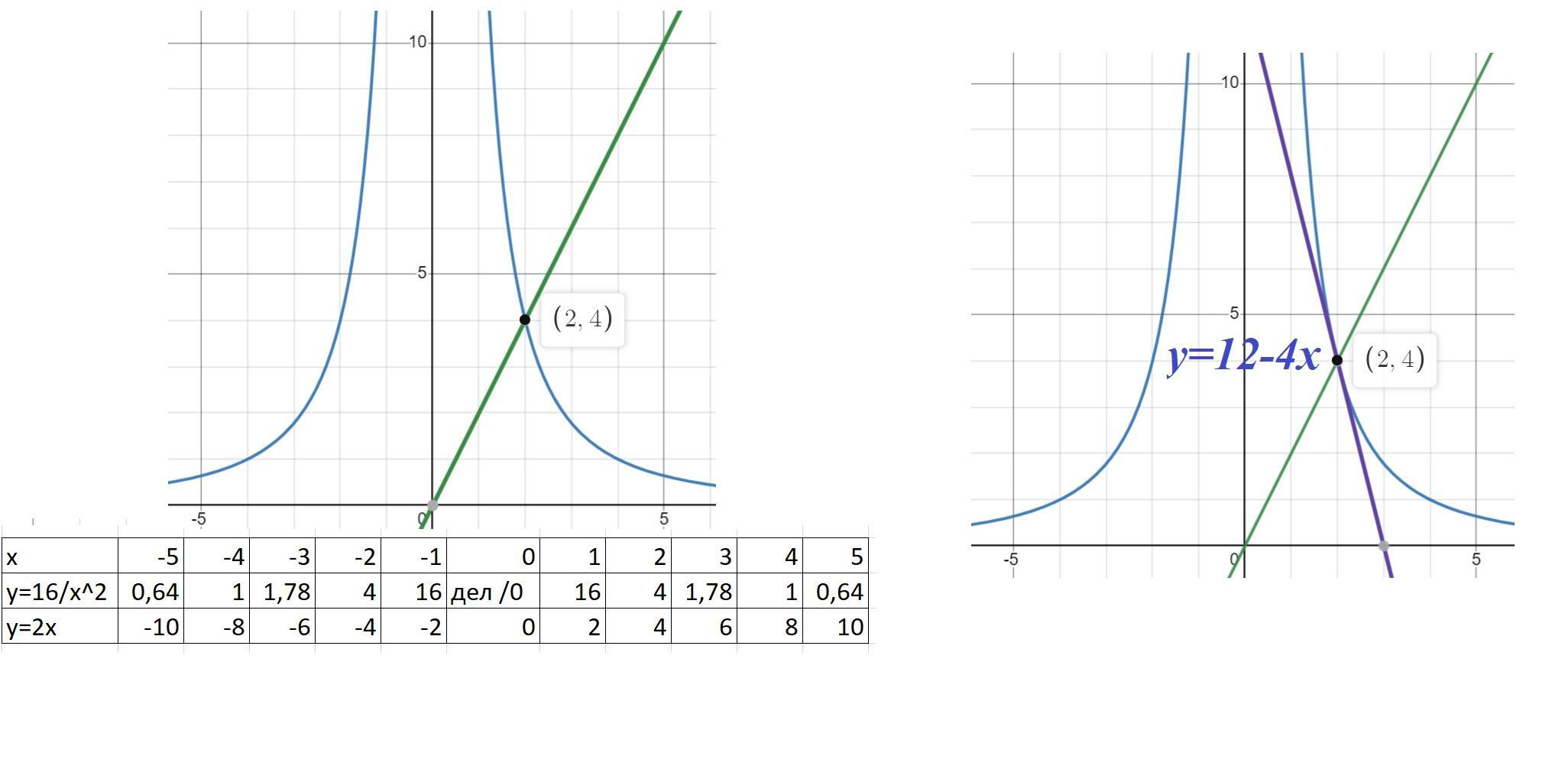
Найдите уравнение касательной к кривой у=16/х² проведенной в точке пересечения ее с прямой у = 2х.

Answer 1

Ответ:  y=-4x+12.

Пошаговое объяснение:

у=16/х²;   у = 2х.

Найдем точку A пересечения графиков

16/x^2 = 2x;

16=2x^3;

x^3=8;

x=2.

y=2x = 2*2 = 4.

A(2;4).

*********************

y=f(x0) + f'(x0)(x-x0).

f(2) = 16/(2^2) = 16/4 = 4.

f'(x) = (16/x^2)' = -32/x^3;

f'(2)=-32/(2^3) = -32/8 =-4.

Уравнение касательной к графику функции f(x) в точке x0=2 имеет вид  y=f(x0) + f'(x0)(x-x0). Подставляем x0=2 =>

y=4+(-4(x-2)) = 4-4x+8 = 12-4x.

y=-4x+12.

(См. скриншот).