Помогите пожалуйста,фото внизу. С объяснением пожалуйста
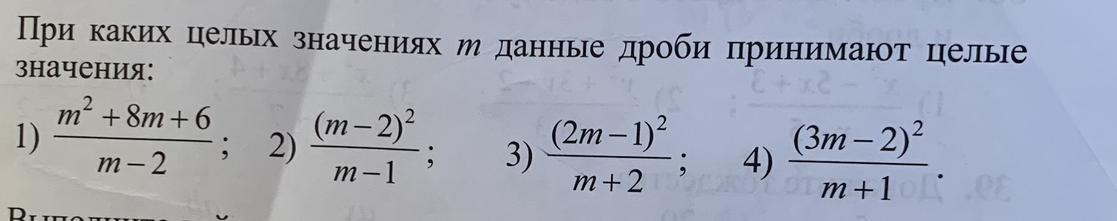
Ответы
Ответ:
Объяснение:
Все выражение целое число , если дробь 26/(m-2) - целое число.
Это выполняется при m=-11, m=0 ; m=1 ; m=3 ;m=4; m=15
Все выражение целое число , если дробь 1/(m-1) - целое число.
Это выполняется при m=0 ; m=2
Все выражение целое число , если дробь 25/(m+2) - целое число.
Это выполняется при m=-27 ; m=-7 ; m=-3 ; m=-1 ; m=3; m=23
Все выражение целое число , если дробь 25/(m+1) - целое число.
Это выполняется при m=-26 ; m=-6 ; m=-2 ; m=0 ; m=4; m=24
Надо разделить числитель на знаменатель.
Остаток должен быть целым числом.
1) m² + 8m + 6| m – 2
m² - 2m m + 10
10m + 6
10m – 20
26.
m² + 8m + 6 = m + 10 + (26/(m – 2)).
Множители числа 26: +-2, +-13, +-26.
1) m – 2 = 2, m = 4.
2) m – 2 = 13, m = 15.
3) m – 2 = 26, m = 28.
4) m – 2 = -2, m = 0.
5) m – 2 = -13, m =-11.
6) m – 2 = -26, m = -24.
Проверка.
1) (4² + 8*4 + 6)/(4 – 2) = (16 + 32 + 6)/2 = 54/2 = 27. Верно.
2) (15² + 8*15 + 6)/(15 – 2) = (225 + 120+ 6)/13 = 351/13 = 27. Верно.
3) (28² + 8*28 + 6)/(28 – 2) = (784 + 224 + 6)/26 = 1014/26 = 39.
Верно.
4) (0² + 8*0 + 6)/(0 – 2) = (0 + 0 + 6)/(-2) = 6/(-2) = -3. Верно.
5) ((-11)² + 8*(-11) + 6)/(-11 – 2) = (121 - 88+ 6)/(-13) = 39/(-13) = -3. Верно.
6) ((-24)² + 8*(-24) + 6)/(-24 – 2) = (784 - 224 + 6)/26 = 390/(-26) = -15.
Верно.
2) (m – 2)²/(m – 1).
m² - 4m + 4|(m – 1)
m² - m m - 3
-3m + 4
-3m + 3
1.
(m – 2)²/(m – 1) = m – 3 +(1/(m – 1)).
m – 1 = +-1.
1) m – 1 = +1, m = 2.
2) m – 1 = -1, m = 0.
Проверка.
1) (2 – 2)²/(2 – 1) = 0. Верно.
2) (0 – 2)²/(0 – 1) = -2/(-1) = 2. Верно.
3) (2m – 1)²/(m + 2).
4m² - 4m + 1|(m + 2)
4m² + 8m 4m - 12
-12m + 1
-12m - 24
25.
(2m – 1)²/(m + 2) = 4m – 12 + (25/(m + 2)).
Множители числа 25: +-1, +-5, +-25.
1) m + 2 = +1, m = -1.
2) m +2 = -1, m = -3.
3) m + 2 = +5, m = 3.
4) m + 2 = -5, m = -7.
5) m + 2 = 25, m = 23.
6) m + 2 = -25, m = -27.
Проверка.
1) (2*(-1) – 1)²/((-1) + 2) = 9/1 = 9. Верно.
2) (2*(-3) – 1)²/((-3) + 2) = 49/(-1) = -49. Верно.
3) (2*3 – 1)²/(3 + 2) = 25/5 = 5. Верно.
4) (2*(-7) – 1)²/((-7) + 2) = 225/(-5) = -45. Верно.
5) (2*23 – 1)²/(23 + 2) = 2025/25 = 81. Верно.
6) (2*(-27) – 1)²/((-27) + 2) = 3025/(-25) = -121. Верно.
Четвёртое задание - аналогично.