Предмет: Алгебра,
автор: sirlemonboy
Вычислить площадь фигуры, ограниченной линиями (предварительно сделав рисунок): y=4x-x^2, y=0, x=5
Срочно нужна помощь!!
Ответы
Автор ответа:
1
Ответ:
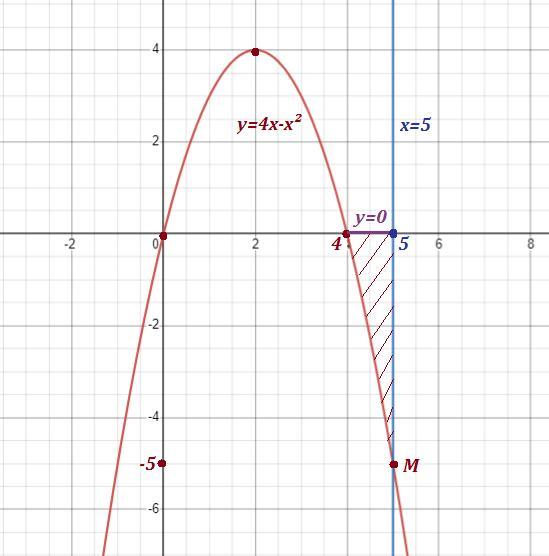
Парабола y = 4x - x² имеет вершину в точке ( 2 ; 4 ) , ветви направлены вниз . Точки пересечения графика с осью ОХ ( у=0 ) имеют коoрдинаты (0;0) и (4;0) .
Точкa пересечения графика параболы с прямой х=5 :
y(5) = 4 · 5 - 5² = -5 ⇒ M ( 5 ; -5 )
Область, площадь которой надо вычислить, заштрихована на рисунке .
Площадь вычисляем, применяя определённый интеграл . Причём перед интегралом надо поставить минус, так как область лежит ниже оси ОХ .
Приложения:
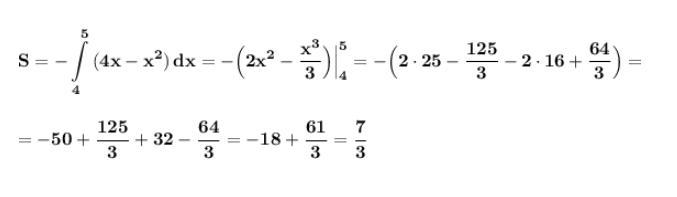
ГАЗ52:
125-64=
а так хорошо на 3 делилось ...
Спасибо
Ага.
Похожие вопросы
Предмет: История,
автор: nkabitkhan
Предмет: История,
автор: arslanbaisugur15
Предмет: Математика,
автор: tazabaevikram
Предмет: Химия,
автор: mexaytka
Предмет: Русский язык,
автор: kazy92306kazy92306