помогите с решением
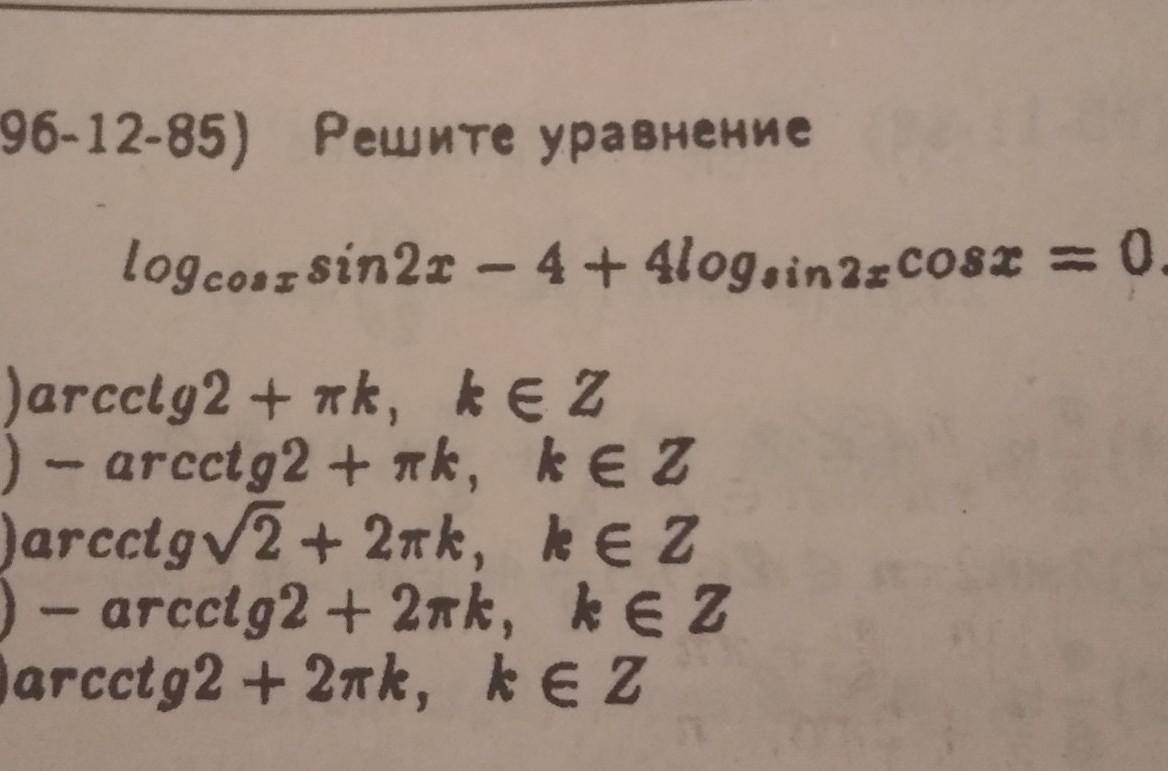
Ответы
Відповідь: 1 - а відповідь : arcctg2 + πk , kЄ Z .
Пояснення:
log(cosx) sin2x - 4 + 4log(sin2x)cosx = 0 ; у 3 - му доданку після
переходу до логарифма за основою сosx і множення рівняння
на log(cosx) sin2x ≠ 0 матимемо рівняння :
log²(cosx) sin2x - 4log(cosx) sin2x + 4 = 0 . Заміною z = log(cosx) sin2x
воно зведеться до квадратного рівняння :
z² - 4z + 4 = 0 ;
( z - 2 )² = 0 ;
z = 2 . log(cosx) sin2x = 2 ;
cos²x = sin2x ;
cos²x - 2sinxcosx = 0 ;
cosx( cosx - 2sinx ) = 0 ;
cosx = 0 ; або cosx - 2sinx = 0 ;
не піходить як основа сosx = 2sinx ;
логарифма . сtgx = 2 ;
x = arcctg2 + πk , kЄ Z .
В - дь : arcctg2 + πk , kЄ Z .