Question

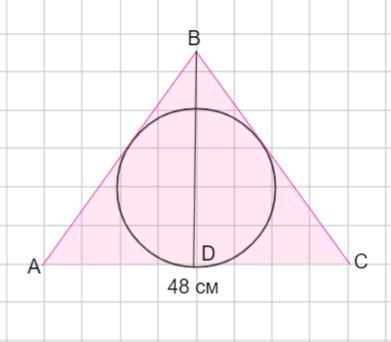
Основа рівнобедреного трикутника дорівнює 48 см, а його площа - 432 см2 . Знайдіть радіус кола, вписаного в трикутник з малюнкоммм

Answer 1

Ответ:

8 см .

Объяснение:

Основание равнобедренного треугольника равно 48 см, а его площадь 432 см ². Найти радиус окружности, вписанной в треугольник.

Пусть дан ΔАВС - равнобедренный ( АВ = ВС) , АС =48 см. Проведем высоту BD , проведенную к основанию. В равнобедренном треугольнике она является биссектрисой и медианой.

Площадь треугольника равна полупроизведению стороны на высоту, проведенную к этой стороне

$S =\dfrac{1}{2} \cdot AC \cdot BD;\\\\BD =\dfrac{2S}{AC} ;\\\\BD =\dfrac{2\cdot 432}{48} =\dfrac{2\cdot 48\cdot 9 }{48} =18$

Значит, высота BD =18 см. Если BD - медиана, то АD=СD= 48: 2 = 24 см.

Рассмотрим ΔАBD - прямоугольный. Найдем гипотенузу АВ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

АВ ² = АD² +BD²;

АВ ²= 24² + 18² = 576 +324 = 900;

АВ =√900 = 30 см.

Значит, АВ =ВС = 30 см.

Периметр треугольника - это сумма длин всех сторон треугольника

Р= АВ +ВС +АС ;

Р =30 +30 +48 =108 см

Радиус окружности, вписанной в треугольник, найдем по формуле:

$r=\dfrac{2S}{P} ,$   где S - площадь треугольника, а  P - периметр треугольника.

$r=\dfrac{2\cdot 432}{108} =\dfrac{2\cdot 4\cdot108}{108} =8$

Значит, радиус окружности, вписанной в треугольник, равен 8 см.