Предмет: Математика,
автор: andrejbaza26
Составить уравнение касательной и нормали к кривой f(x) в точке хо СРОЧНО ПОЖАЛУЙСТА
Приложения:
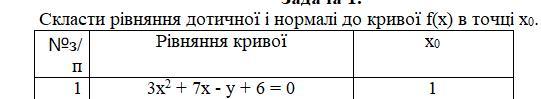
Ответы
Автор ответа:
3
Уравнение касательной к кривой в точке
имеет вид:
Уравнение нормали к кривой в точке
имеет вид:
По условию заданы уравнение и точка:
Выразим через
:
Найдем производную:
Найдем значение функции и ее производной в точке:
Составляем уравнение касательной:
Составляем уравнение нормали:
Похожие вопросы
Предмет: Литература,
автор: chychelolala
Предмет: Английский язык,
автор: katrinalaura825
Предмет: Литература,
автор: mashukaa
Предмет: Обществознание,
автор: anna174517