математический анализ 1 курсы. Последовательности
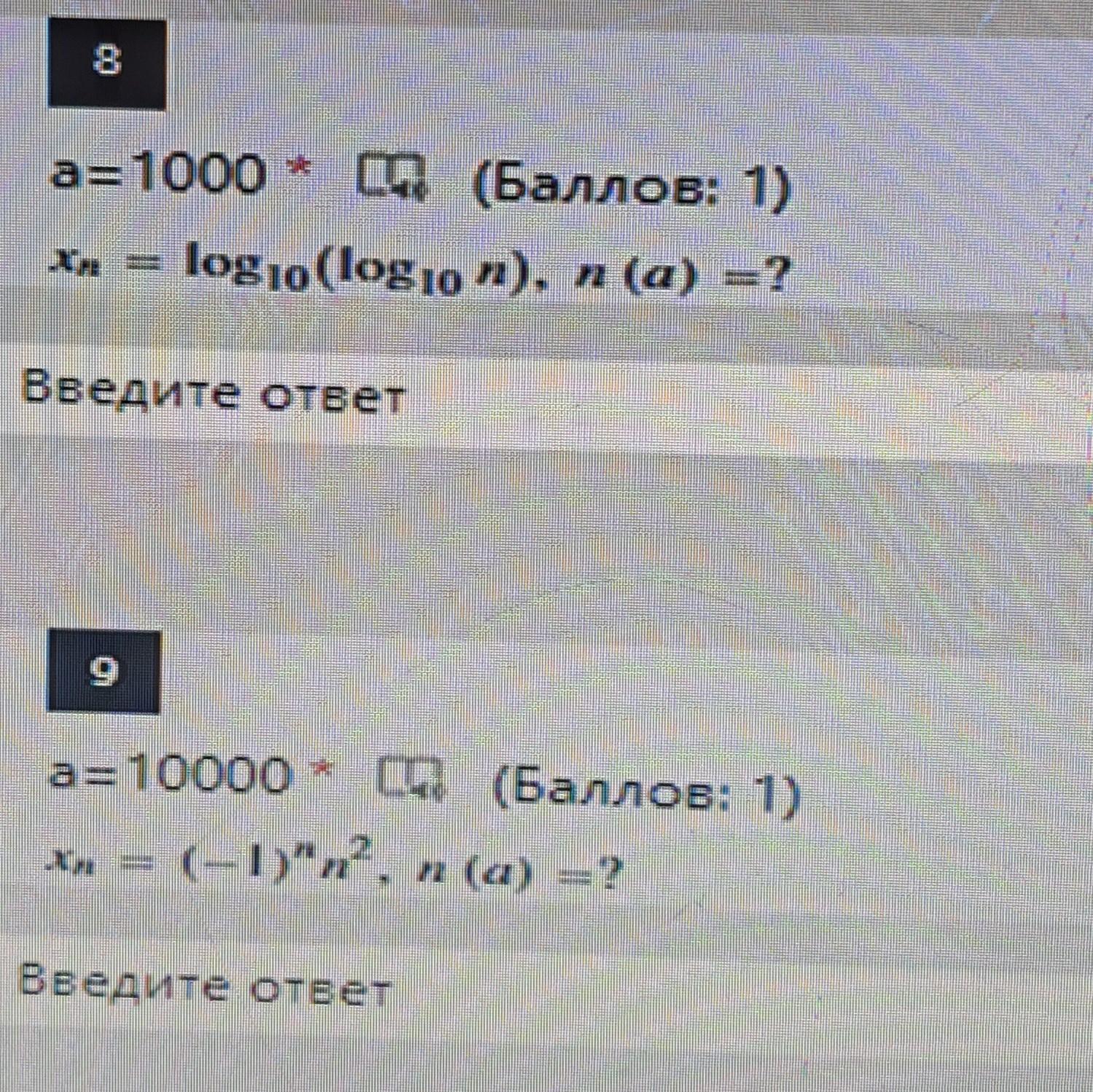
Ответы
Ответ:
1.Чтобы найти значение n (a) для заданной последовательности xn = log10(log10 n), нам нужно подставить a = 1000 в уравнение и решить для n.
Учитывая xn = log10(log10), мы имеем:
log10(лог10) = a
Подставляя a = 1000:
log10(лог10) = 1000
Чтобы решить для n, мы сначала исключим логарифмы.
Шаг 1: Поднимите обе стороны в степени 10:
10^(log10(лог10)) = 10^1000
Это упрощает работу с:
log10 = 10^1000
Шаг 2: Снова увеличьте обе стороны до степени 10:
10^(log10) = 10^(10^1000)
Это еще больше упрощает задачу:
n = 10^(10^1000)
Следовательно, значение n (a) равно 10^(10^1000).
2.Чтобы найти значение n (a) для заданной последовательности xn = (-1)^(n ^ 2), где a = 10000, нам нужно подставить a в уравнение и решить для n.
Учитывая xn = (-1)^(n ^ 2), мы имеем:
(-1)^(n^2) = a
Подставляя a = 10000:
(-1)^(n^2) = 10000
Чтобы решить для n, мы можем извлечь квадратный корень из обеих сторон:
sqrt((-1)^(n^2)) = sqrt(10000)
С левой стороны квадратный корень из (-1) ^(n ^ 2) равен либо 1, либо -1, поскольку (-1) ^(n ^ 2) чередуется между положительными и отрицательными значениями по мере увеличения n. Таким образом, у нас есть:
1 или -1 = 100 или -100
Это означает, что в данной последовательности не существует реального значения n, удовлетворяющего уравнению для a = 10000.