Question

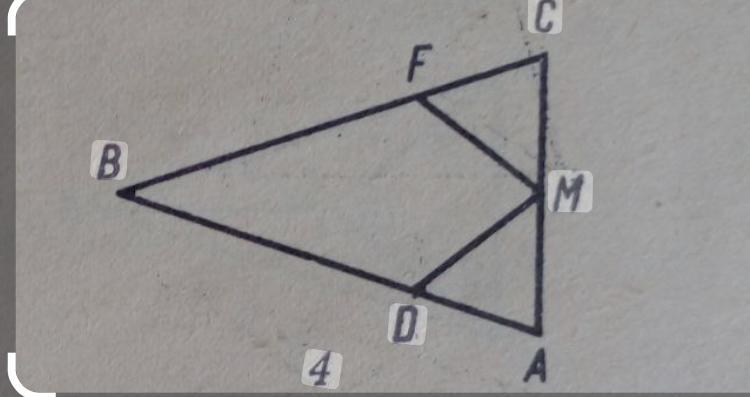
дано: AB = CB, AD = CF, M - середина АС.

Довести: MD = MF.

Answer 1

Відповідь:

АВ=СВ,значит это равнобедренный треугольник.,Боковые стороны треугольника -катеты-АВи СВ,значит АС-основание.

В равнобедренном треугольнике углы при основании равны             Значит уголА=уголС.

Середина основания АС -точка М ,делит ее на равные участки МС=АМ,  СF=AD, AM=MC(по условию).две  стороны равны;

значит мы имеет два  треугольника FCM =DAM,у которых  равны две стороны,углы C =A  

Значит,мы имеет равность треугольников по сторанам и углам

Следовательно треугольники FCM =DAM равны по углу и двум сторонам, следовательно, MD =MF

Пояснення: