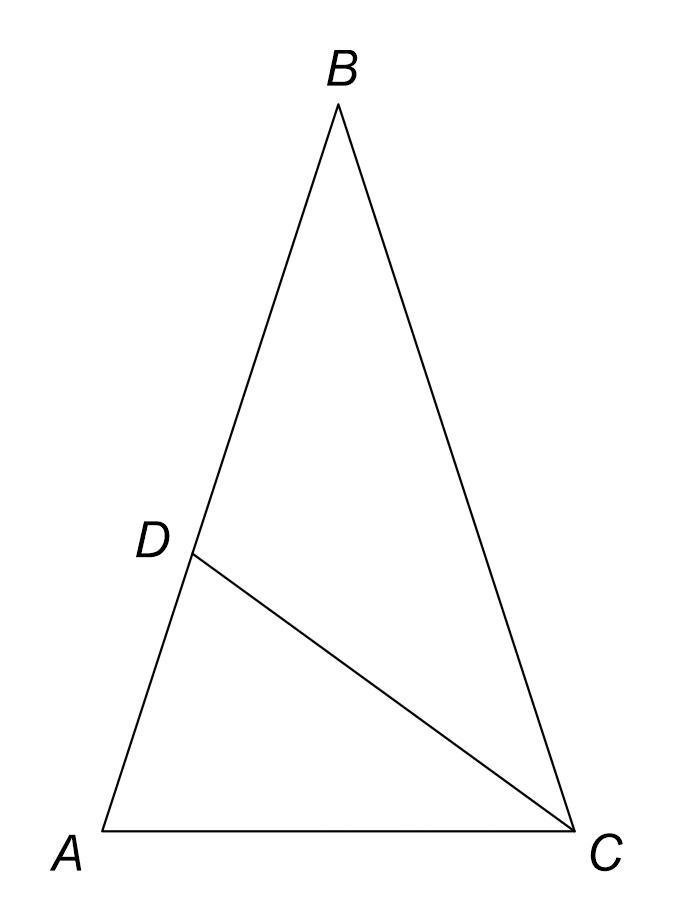
помогите пжжжжжжжжжжжж

Ответы
Ответ:
∠CDB = 108°
Пошаговое объяснение:
Т.к. ΔABC равнобедренный, то у него углы при основании равны.
⇒ ∠BAC = ∠BCA. Обозначим их как x.
Оставшийся угол ∠ABC обозначим как y.
Как известно - сумма углов любого треугольника равна 180°,
⇒ ∠BAC + ∠BCA + ∠ABC = 180°, или:
x + x + y = 180°
2x + y = 180
Т.к. CD биссектриса угла ∠BCD, которая делит его пополам,
⇒ ∠BCD = ∠ACD = ∠BCA/2 = x/2.
Рассмотрим ΔADC - это равнобедренный треугольник, т.к. CD = AC (по условию задачи). А как известно, в равнобедренном треугольнике углы при основании равны ⇒ ∠ADC = ∠DAC = x
Рассмотрим ∠ADC и ∠CDB - это смежные углы, которые в сумме дают 180° ⇒ ∠ADC + ∠CDB = 180°
⇒ ∠CDB = 180° - ∠ADC, или
∠CDB = 180 - x
Рассмотрим ΔBCD. У него:
∠BCD = x/2
∠CDB = 180 - x
∠DBC = y
Как известно - сумма углов любого треугольника равна 180°,
⇒ ∠BCD + ∠CDB + ∠DBC = 180°, или
x/2 + 180 - x + y = 180°
x + 360 - 2x + 2y = 360
2y - x = 0
Получили систему из двух уравнений:
Выведем чему равен y из первого уравнения:
y = 180 - 2x
Подставим полученное значение y во второе уравнение, и найдём чему равен x:
2·(180 - 2x) - x = 0
360 - 4x - x = 0
360 - 5x = 0
5x = 360
x = 360/5
x = 72°
Т.к. ранее мы вывели что ∠CDB = 180° - x
Подставим полученное значение x, и найдём чему равен ∠CDB:
∠CDB = 180° - 72° = 108°