Предмет: Математика,
автор: okayimkate
Найти производные функций. Помогите пожалуйста!
б) y = (cos x)/(1 + sin x)
в) y = 2 ^ x * cos x
Ответы
Автор ответа:
1
Ответ:
Найти производные функций. Воспользуемся правилами дифференцирования функций .
Приложения:

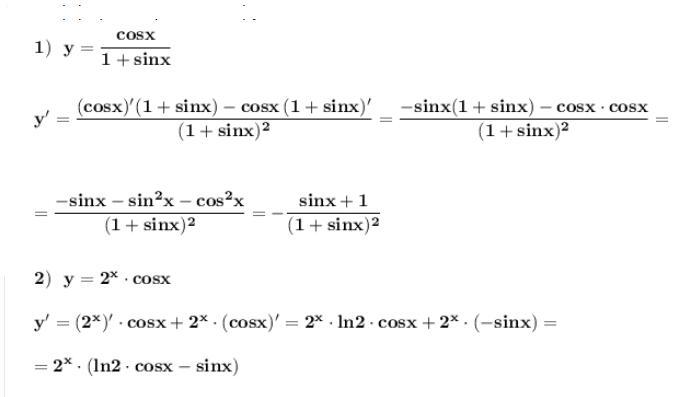
Похожие вопросы
Предмет: География,
автор: julia0912
Предмет: Химия,
автор: rrprrrr8
Предмет: Химия,
автор: muzinta1977
Предмет: Английский язык,
автор: fenty82