Предмет: Математика,
автор: dimabaxov222
Объясните пожалуйста
Почему в этих примерах после x=(-1) в степени пишется n+1, в каком случае пишется просто n
Приложения:
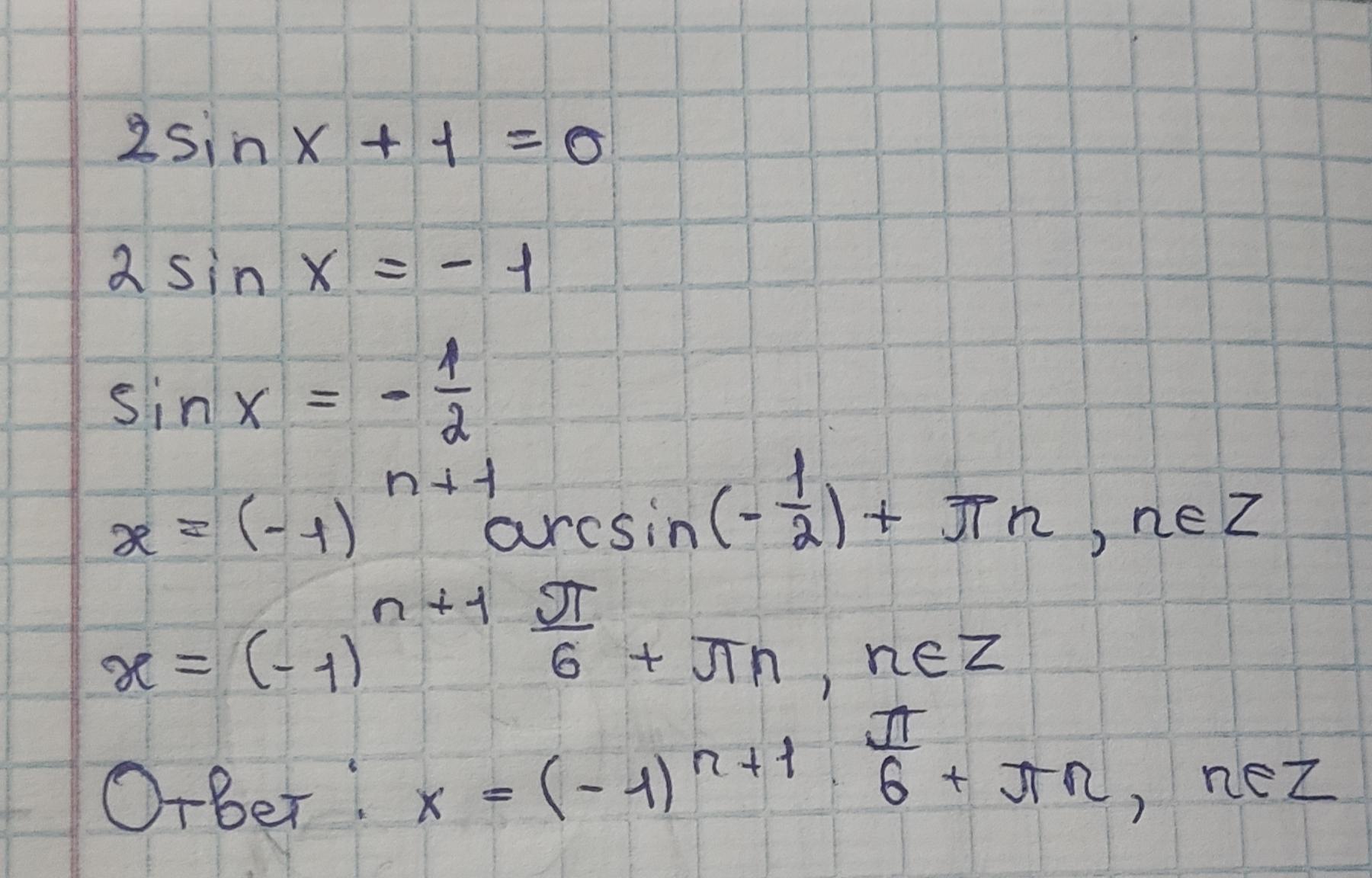

sinx = -1/2
Х=(-1)^n• arcsin(-1/2)+πn , nez
Х=(-1)^n•(- arcsin(1/2))+πn , nez
Х=(-1)^n•(-1)^1• arcsin(1/2)+πn , nez
Х=(-1)^(n+1)• arcsin(1/2)+πn , nez
и тд...
Х=(-1)^n• arcsin(-1/2)+πn , nez
Х=(-1)^n•(- arcsin(1/2))+πn , nez
Х=(-1)^n•(-1)^1• arcsin(1/2)+πn , nez
Х=(-1)^(n+1)• arcsin(1/2)+πn , nez
и тд...
Ответы
Автор ответа:
2
Решение.
Известная формула решения уравнения :
Если число a отрицательно , то есть a<0 , то надо учитывать ещё нечётность функции y=arcsin x и применить свойство :
arcsin(-a) = -arcsin a . А затем воспользоваться свойством степени : .
Например ,
Приложения:

Похожие вопросы
Предмет: Математика,
автор: pikust228
Предмет: Математика,
автор: asyaaads
Предмет: Обществознание,
автор: f6k92bz7h5
Предмет: Математика,
автор: anastasiasokolova191
-Sinx =√3/2
sinx = -√3/2
Х=(-1)^n• arcsin(-√3/2)+πn , nez
Х=(-1)^n•(- arcsin(√3/2))+πn , nez
Х=(-1)^n•(-1)^1• arcsin(√3/2)+πn , nez
При умножении степеней с одинаковым основание ( в данном случае основание (-1) ), основание остаётся прежним, а степени складываются.
Х=(-1)^(n+1)• arcsin(√3/2)+πn , nez
и тд...