Question

СРОЧНО РЕШЕНИЕ С ФОТО И РИСУНКОМ!!!
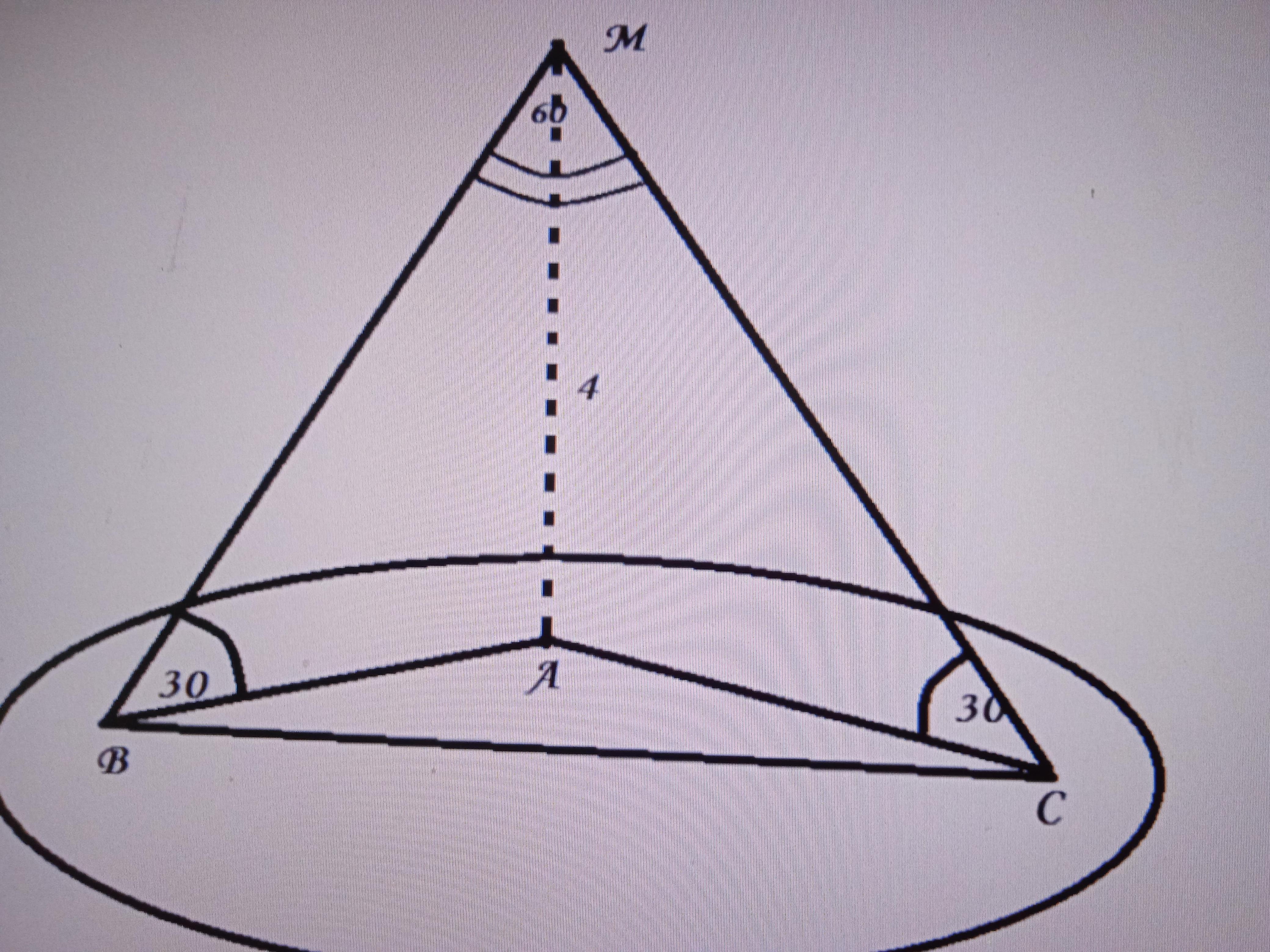
Из точки M к плоскости a проведены две наклонные, которые образуют со своими проекциями на плоскость a углы 30°. Угол между наклонными равен 60°. Найдите расстояние основаниями наклонных, если расстояние от точки M до точки a равно 4 см.

Answer 1

Ответ: 8 cm

Объяснение:  см файл

f453de64f071c066e26645321b383bb8.pdf

Answer 2

Ответ:

8 cм.

Объяснение:

Дано: ВМ и СМ - наклонные,  АМ⊥плоскости α;  АМ=4 см. ∠МВА=∠МСА=30°.   ВС-?

ΔАСМ - прямоугольный, АМ=4 см, ∠АСМ=30°, значит СМ=2АМ=8 см по свойству катета, лежащего против угла 30°

Аналогично ΔАВМ,  ВМ=8 см.

ΔВМС - равнобедренный, ∠МВС=∠МСВ=(180-60):2=60°, значит

ΔМВС - равносторонний и ВС=ВМ=СМ=8 см.