Предмет: Геометрия,
автор: veronikA228111111111
В треугольнике АВC проведены высоты ВB1 и СС1. Докажите, что касательная в точке А к описанной окружности параллельна прямой В1С1, а В1C1 перпендикулярна ОА (О - центр описанной окружности).
cos20093:
"Настоящее" решение этой задачки выглядит так. B1C1 антипараллельна BC, ВС перпендикулярна высоте AA1, OA изогонально сопряжена AA1, касательная в точке A к описанной окружности перпендикулярна OA => эта касательная тоже антипараллельна BC => B1C1 параллельна этой касательной и перпендикулярна OA. "Преумножая знания, преумножаешь ..." и так далее
везде, где употребляется слово "антипараллельна", следует читать "антипараллельна относительно угла A", чтобы быть точным
Переводя это все на понятный язык, получается вот что. Если отразить симметрично OA, перпендикулярную OA касательную в точке A и B1C1 относительно биссектрисы угла A, то OA перейдет в AA1, а B1C1 станет параллельной BC, откуда следует ответ.
Меня иногда спрашивают, зачем я пишу "подобное" для тех, кому это явно не нужно? Отвечаю. А - вдруг? Вдруг у кого-то вместо GPT4 в голове проявится свой, естественный интеллект? Вероятность этого есть... Это не так и много - возьмите книжку Д. Ефремова 1902 года и посмотрите, как учили геометрии тогда. Кстати, я тоже не корифей в геометрии, просто кое-что читал и иногда люблю порешать задачки чуть сложнее средних школьных.
справедливости ради: по Ефремову не учили. И по Зетелю не учили. Это факультатив, публикации в профильных журналах, собранные в труды. Так то, если собрать Квант, получим отличную геометрию.
Ответы
Автор ответа:
0
Отрезок BC виден из точек B1 и C1 под прямым углом
- точки B C1 B1 C лежат на окружности диаметром BC.
BC1B1C - вписанный четырехугольник.
Внешний угол вписанного четырехугольника равен противолежащему внутреннему.
∠AB1C1=∠ABC
Угол между касательной и хордой равен половине дуги, стягиваемой хордой.
∠KAC=◡AC/2=∠ABC
∠AB1C1=∠KAC => накрест лежащие углы равны, AK||B1C1
Радиус в точку касания перпендикулярен касательной.
OA⊥AK => OA⊥B1C1
Приложения:
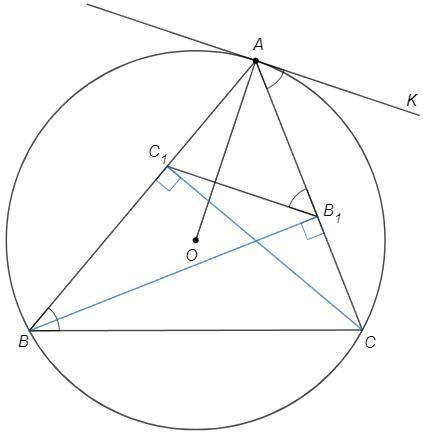
По этой конфигурации надо знать: AB1C1~ABC, k=cosA
Кстати, есть совершенно прямой способ показать это в одно действие. В самом деле, AC1 = AC*cosA; AB1 = AB*cosA; и это все - две стороны пропорциональны и угол общий, коэффициент пропорциональности cosA
Тут восприятию мешает, что "треугольник перевернут". Такой "оптический обман". Для робота или ИИ здесь вообще не было бы причины для недопонимания. А у человека возникает некий стопор.
Похожие вопросы
Предмет: Алгебра,
автор: veri5494
Предмет: Химия,
автор: andrewgolub911
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: mokrakovaviktoria75