Предмет: Алгебра,
автор: dddus
Вычислите предел функции
Приложения:
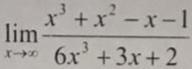
Ответы
Автор ответа:
2
Преобразовываем выражение
(надпись x→∞ немного съехала, пиши ее под лимитом)
Теперь подставляем бесконечность вместо х:
Бесконечность хоть в квадрате, хоть в кубе, все равно останется бесконечностью, а число, деленное на бесконечность, будет равно нулю, значит
Ответ:
dddus:
В преобразовываем выражении не видно продолжения
с телефона?
Да
С компьютера посмотрю
переверни телефон на бок или свайпом открой продолжение
Похожие вопросы
Предмет: Биология,
автор: kolakin2229
Предмет: Другие предметы,
автор: kolesnik18
Предмет: Алгебра,
автор: igorr79
Предмет: Математика,
автор: Vv65
Предмет: Математика,
автор: Alxazovakemale