Предмет: Геометрия,
автор: aarr04594
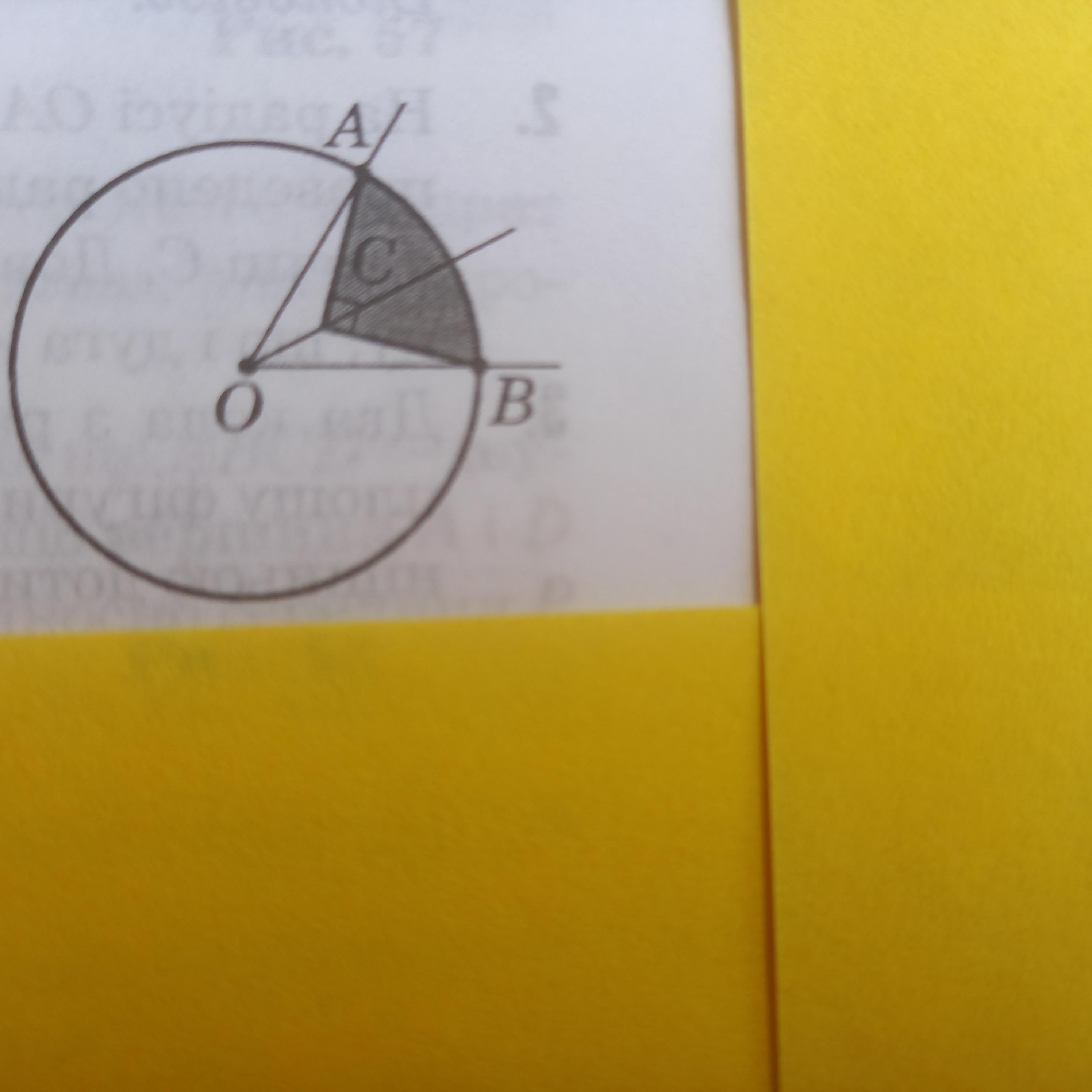
Зовні прямого кута з вершиною С на продовженні його бісектриси взято точку О таку, що ОС=√2. З центром в точці О побудовано коло з радіусом 2. Знайти площу фігури , обмеженої сторонами кута і дугою кола, що розташована між ними.
Приложения:
experced:
короче надо найти площадь заштрихованный фигуры, да?
Так
Кроки розв'язання. Від площі сектора ОАВ відняти суму площ трикутників ОАС і ОВС. За т.синусів визначаємо кут ОАС=30°. Тоді кут АОС =15°. Визначаємо площу трикутників , вона становить |/2×sin15°. За допомогою формули sin різниці аргументів знаходимо значення sin15°.
Спосіб цікавий. Можливо після знаходження кута АОС=15° простіше перейти до кута АОВ і далі працювати з теоремою косинусів, але це моя суб'єктивна думка
Можливо. Все красиво.
Погано, що немає такої опції " додати своє розв'язання ".
Сам питання задав, сам відповів? А що, запропонуйте свою ідею розробникам, а то вони лише питають, що можна покращити...
Ответы
Автор ответа:
2
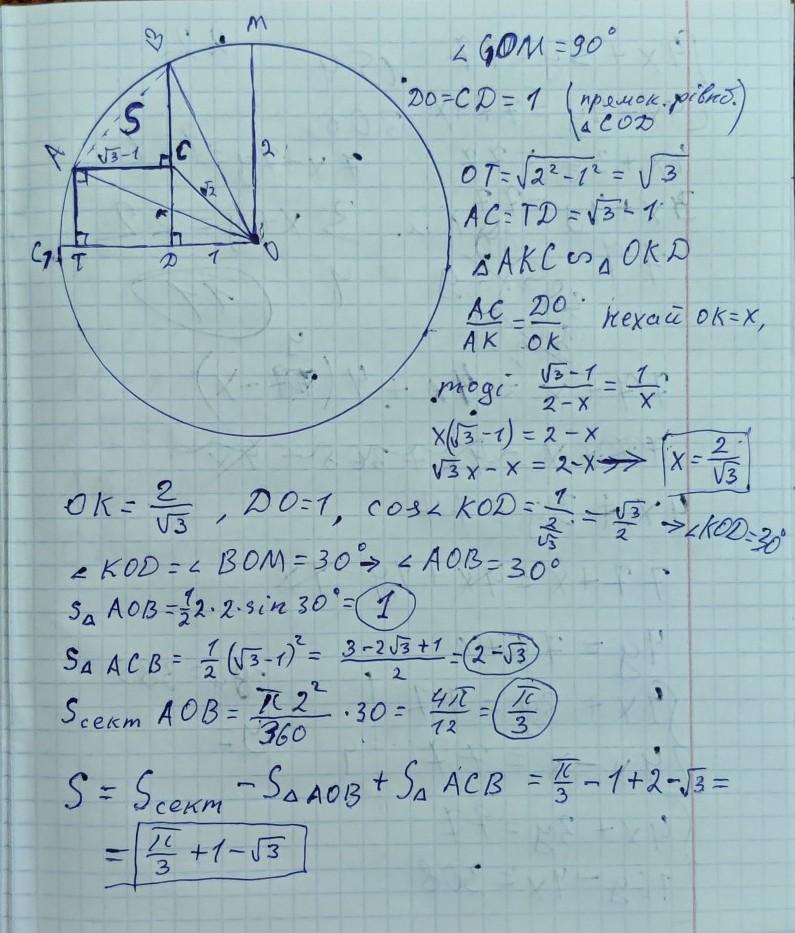
Ответ:
π\3+1-√3
Объяснение:
розв'язання задачі на фото.
відповідь не дуже сподобалась, може десь помилився?
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: shukinartem1103
Предмет: Физика,
автор: fantom023575
Предмет: Математика,
автор: monosovevgenij9
Предмет: Математика,
автор: artemgamurov26