Предмет: Геометрия,
автор: arsenyokulenko
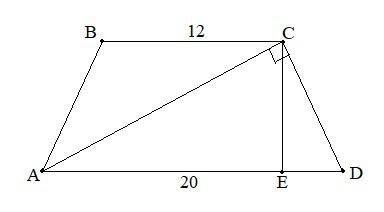
В равнобедренной трапеции АBCD основания BC и AD соответственно равны 12 см и 20 см. Найдите площадь трапеции, если ее диагональ АС перпендикулярна боковой стороне CD.
zmeura1204:
128
Ответы
Автор ответа:
1
Ответ:
CE - высота трапеции ABCD и ∆ACD.
DE - проекция катета CD.
AE - проекция катета AC.
DE = (AD - BC)/2 = (20 - 12)/2 = 4 см.
AE = AD - DE = 20 - 4 = 16 см.
CE = √(AE * DE) = √(16 * 4) = √64 = 8 см.
Sтрапеции = 1/2(AD + BC) * CE = 1/2 * (20 + 12) * 8 = 128 см^2.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: liknastya7
Предмет: Физика,
автор: kyleshova027
Предмет: Українська мова,
автор: zmihail2406
Предмет: Химия,
автор: danilleontiv2002