Предмет: Геометрия,
автор: valiahmetov859
Помогите с аналитической геометрией
Приложения:
Ответы
Автор ответа:
2
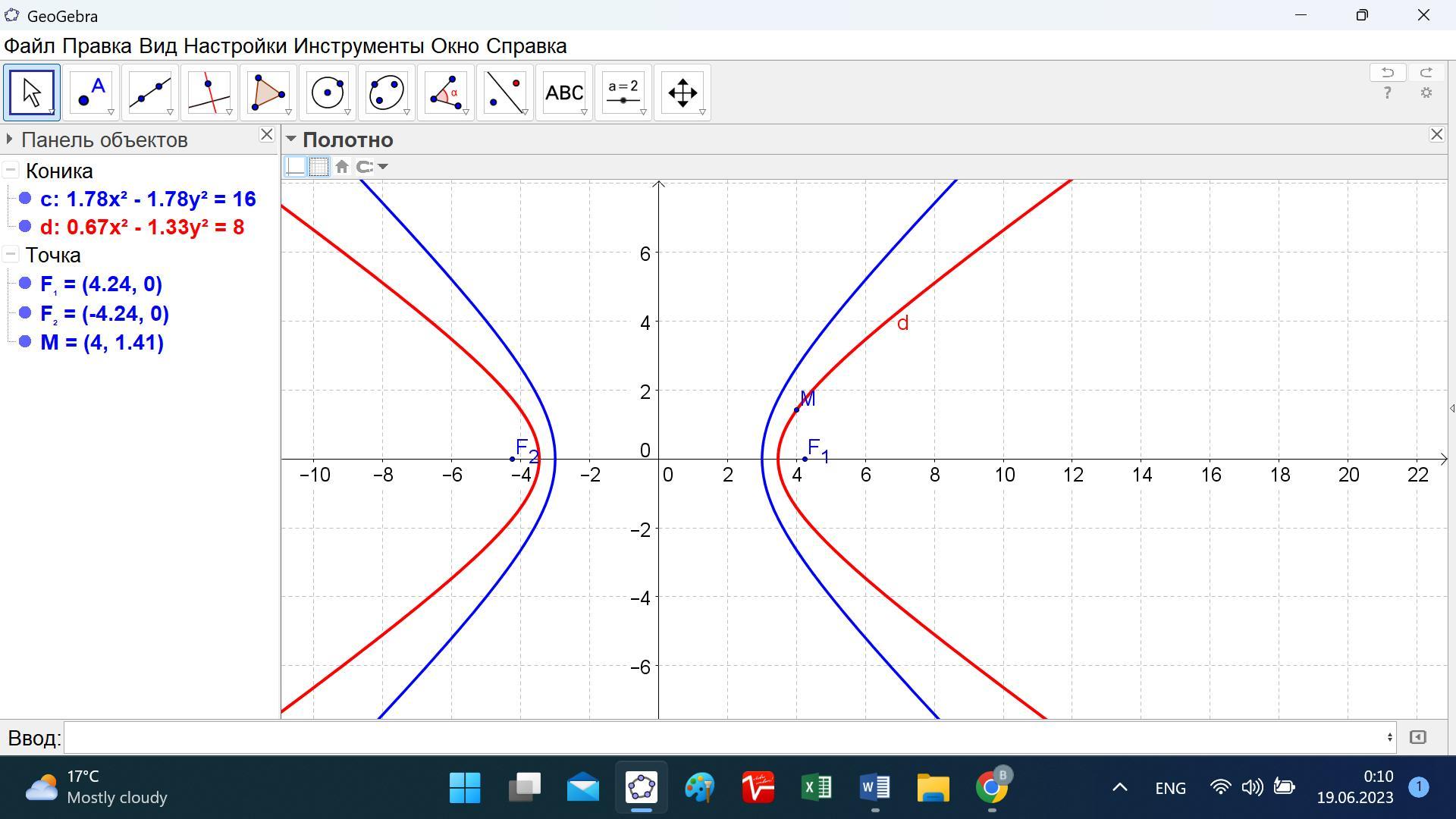
Заданная гипербола имеет центр в начале координат с осями a = b = 3.
Находим расстояние с от центра до фокуса.
с = √(3² + 3²) = √18 = 3√2.
Используем для второй гиперболы свойство c² = a² + b².
Тогда уравнение её будет (x²/a²) – (y²/(18 – a²)) = 1.
Подставим координаты точки М(4; √2).
(16/a²) – (2/(18 – a²)) = 1.
(16(18 – a²)) - 2a² = a² (18 – a²)).
С положительным знаком имеем 2 решения: а = 2√3 и а = 2√6.
Находим квадрат мнимой оси: b² = c² - a² = 18 – 12 = 6.
Для второго варианта b² = c² - a² = 18 – 24 = -6 решение не принимаем.
Ответ: уравнение второй гиперболы будет
(x²/(2√3)²) – (y²/(√6)²) = 1.
Приложения:
Похожие вопросы
Предмет: История,
автор: holikovaelvira2308
Предмет: Другие предметы,
автор: e31997497
Предмет: Українська мова,
автор: valeriiiaa0
Предмет: Алгебра,
автор: hvanrts2153
Предмет: Алгебра,
автор: fesbhjlmk