Question

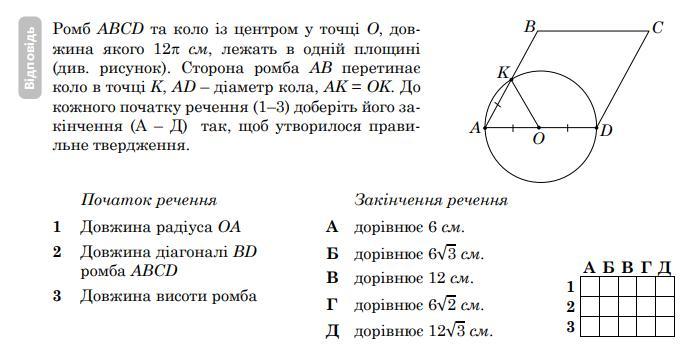
Ромб ABCD та коло із центром у точці O, довжина якого 12 см, лежать в одній площині
(див. рисунок). Сторона ромба AB перетинає
коло в точці K, AD – діаметр кола, AK = OK. До
кожного початку речення (1–3) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Answer 1

Ответ:

1)А

2)B

3)Б

Объяснение:

1)

длинна круга: С=2πr

тогда:

$12\pi = 2r\pi \\ r = \frac{12\pi}{2\pi} \\ r = 6$

следовательно радиус мы нашли

радиусы круга на картинке это: АО, OK, OD

значит длина радиуса ОА = 6 см

2)

найдем сторону ромба, она равна диаметру круга, значит:

6×2=12 см - сторона ромба

треугольник ОАК - равносторонний, так как одна сторона равна радиусу круга, а две вторые являются диаметрами того же круга. следовательно угол BAD = 60°

тгода найдем меньшую диагональ по формуле:

d=a√(2-2cosa)

$d = 12 \sqrt{2 - 2 \cos(60) } \\ d = 12 \sqrt{2 - 2 \times \frac{1}{2} } \\ d = 12 \sqrt{2 - 1 } \\ d = 12$

следовательно мы нашли ответ на второй вопрос

3)

для высоты используем формулу:

h=a×sina

тогда:

$h = 12 \times \sin(60) \\ h = 12 \times \frac{ \sqrt{3} }{2} \\ h = 6 \sqrt{3}$

найден ответ на последний вопрос

Answer 2

Відповідь: фото.

Пояснення:

розв'язання завдання 17 НМТ