Предмет: Математика,
автор: zxcakumaqe
Lim
Обчислити границі функцій.
Приложения:
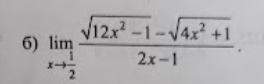
Ответы
Автор ответа:
1
Ответ: =√2
Пошаговое объяснение:
При х -> 1/2 имеем неопредеденность вида 0/0
Чтобы от нее избавиться домножим числитель на сопряженное выражение
Знаменатель тоже домножим на это выражение и получим
Теперь, подставив вместо х =0.5 , получим
2*(2*0.5+1)/(√2+√2)=4/(2√2)=2/√2=√2
zxcakumaqe:
не могли б вы это расписать или в paint или на листке, так будет более понятнее?
Похожие вопросы
Предмет: История,
автор: skuropatnasta677
Предмет: Английский язык,
автор: maksimaskunc
Предмет: Українська мова,
автор: ulianka2445
Предмет: Русский язык,
автор: mifdnoigerigofdombdf
Предмет: Математика,
автор: vikulyaefremenkova