Question

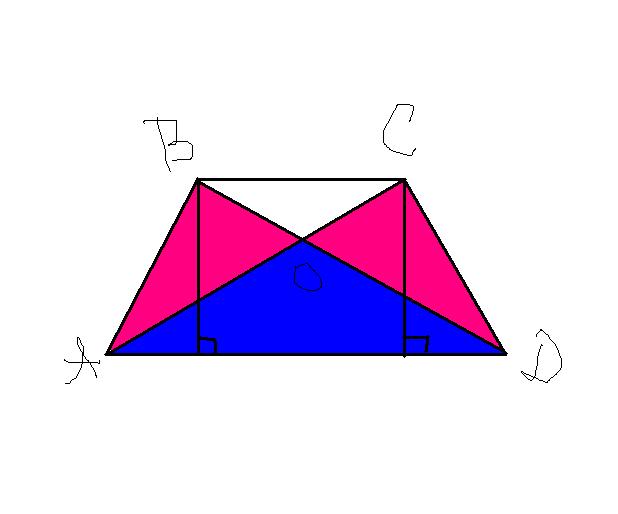
В трапеции ABCD c основаниями AD и BC диагонали пересекаются в точке О. Докажите , что площади треугольников AOB и COD равны.

Answer 1

Пусть AD - нижнее основание AD<BC

S(ABD)=S(ACD) - так как у єтих треугольников общее основание  AD, а высоты треугольников, проведенные к основанию, являются высотами трапеции и потому равны.

 

S(AOB)=S(ABD)-S(AOD)

S(COD)=S(ACD)-S(AOD)

 

поєтому

S(AOB)=S(COD). Доказано