Question

Основою прямої призми є ромб із гострим кутом 60°. Площа більшого діагонального перерізу призми дорівнює 240√3. Обчисліть об'єм призми, якщо її висота дорівнює 8√3?
(Відповідь має бути цілою тобто не 2400√3 або 4800√3)​

Answer 1

Объяснение:

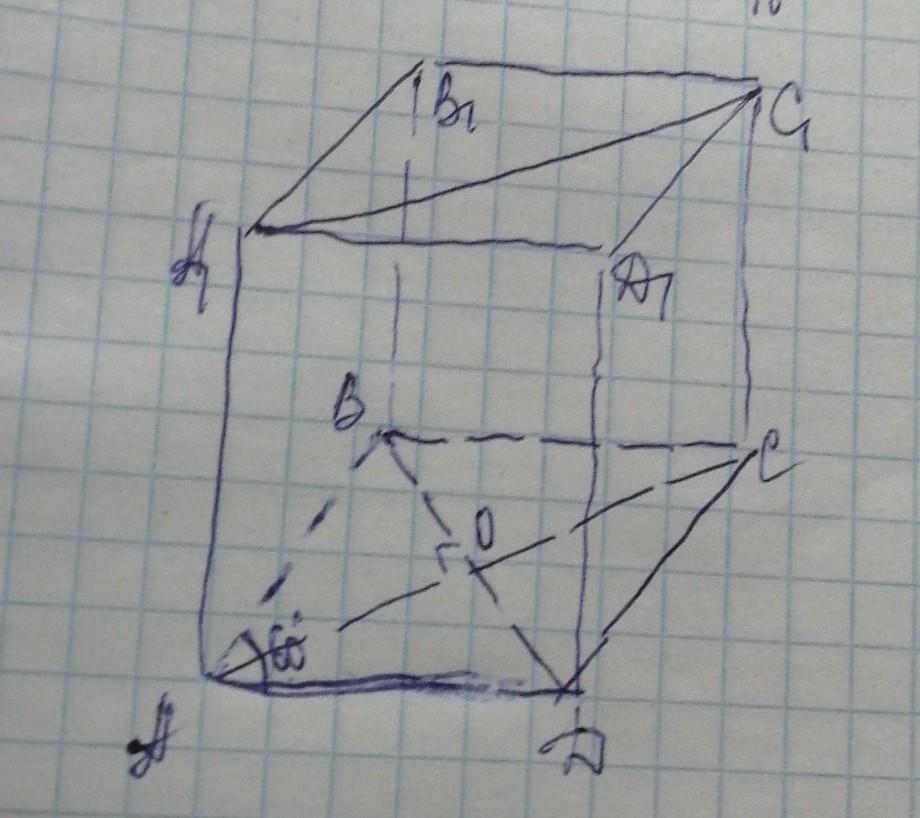
АВСDA1B1C1D1 - призма

АВСD -ромб

∠ВАD=60°

S(AA1C1C)=240√3

AA1=8√3

V=?

S(AA1C1C)=AA1•AC

AC=S(AA1C1C):AA1=240√3:8√3=30

B ромбе диагонали пересекаются под прямым углом и точкой пересечения делятся пополам.

диагонали ромба являются биссектрисами его углов:

∆АОD - прямоугольный:

∠ОАD=∠BAD:2=60:2=30°

АО=АС:2=30:2=15

соs∠OAD=AO/AD

cos30=15/AD

AD=15/(√3/2)=30/√3=10√3

S(ABCD)=AD²•sin∠ABD=(10√3)²•sin60=

=300•(√3/2)=150√3

V=S(ABCD)•AA1=150√3•8√3=3600 ед³

ответ: 3600 ед³