Question

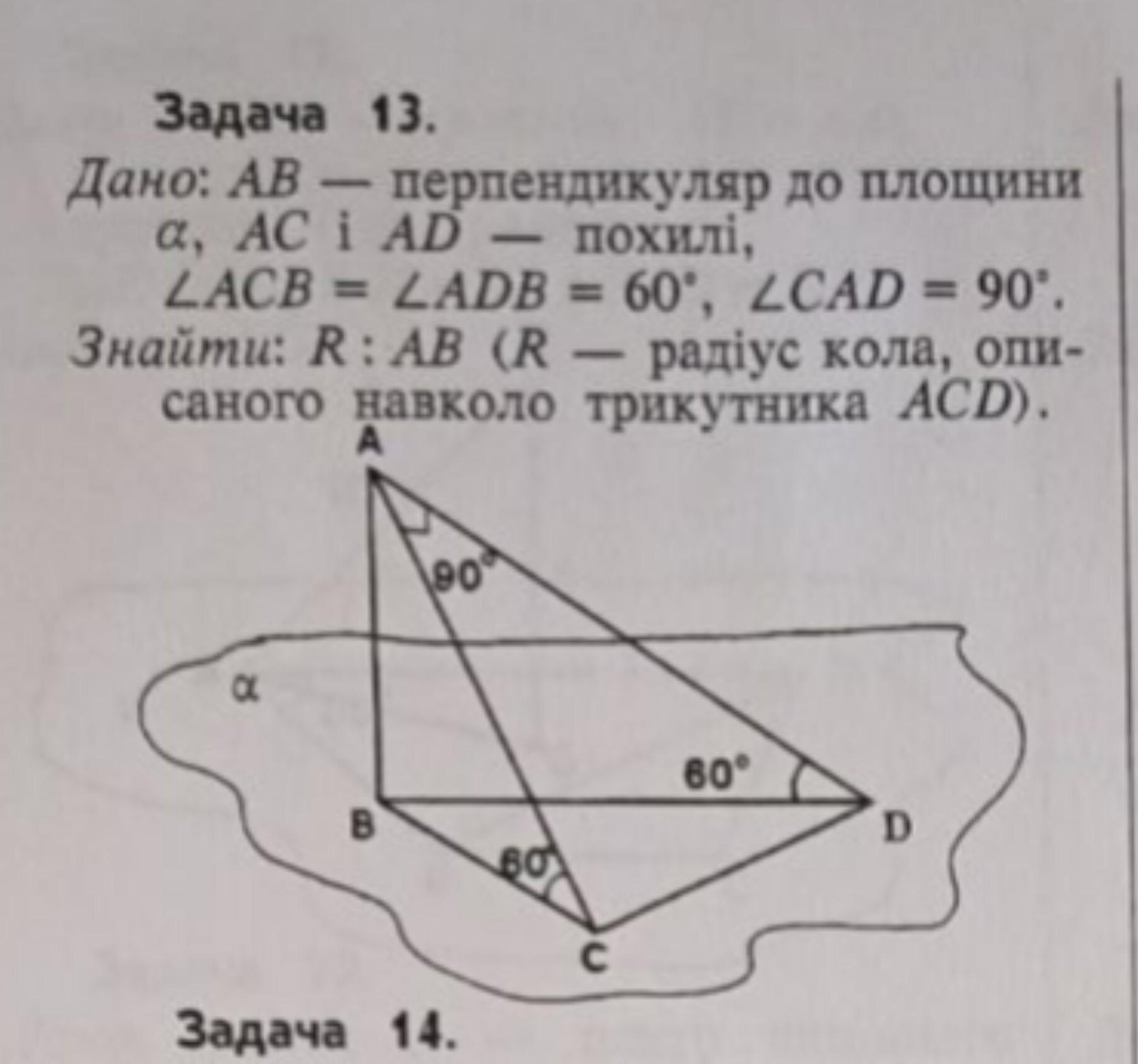
Задача з геометрії
Дано: АВ - перпендикуляр до площини a, АС i AD похилі. кут ACB = кут ADB = 60°, кут СAD = 90'.Знайти: R: АВ (R радіус кола, описаного навколо трикутника ACD).
на фото. Срочно
ДАЮ 50 БАЛОВ
​​

Answer 1

Объяснение:

Спочатку знайдемо сторону трикутника ACD за теоремою Піфагора:

AC² = AD² + CD²

Так як кут СAD = 90°, то з теореми Піфагора для прямокутного трикутника ADC маємо:

AD² + CD² = AC² = AB² + BC², тобто

AB² + BC² - AD² - CD² = 0

За теоремою косинусів в трикутнику ABC, де кут BAC = 90°, маємо:

AB² + BC² = AC² = 2R², де R - радіус описаного кола

Тому маємо рівняння:

2R² - AD² - CD² = 0

R = √[(AD² + CD²)/2]

Далі треба знайти довжину AD та CD. Розглянемо трикутник ACD. Так як кут СAD = 90°, то

sin CAD = CD/AD

З теоремою синусів в трикутнику ACD маємо:

AD/sin 60° = AC/sin CAD = AC/cos 30°

Отже,

AD = AC/(sin 60° cos 30°) = AC/[(1/2)cos 30°] = 2AC/√3

А з теоремою Піфагора для трикутника ACD повторно маємо:

CD² = AC² - AD² = AC² - 4AC²/3 = AC²/3

Тому

R = √[(AD² + CD²)/2] = √[(4AC²/3 + AC²/3)/2] = √[(5/6)AC²]

Таким чином, треба знайти довжину AC. З теоремою Піфагора для трикутника ABC, де кут CAB = 90°, маємо:

AC² = AB² + BC² = 2R²

Отже, AC = R√2. І підставляємо:

R = √[(5/6)(R² * 2)] = √(5/3) * R

Отримали квадратне рівняння відносно R, яке має єдиний додатний корінь:

R = √(15/3) = √5

Відповідь: R = √5.