Предмет: Геометрия,
автор: nastaruduk5
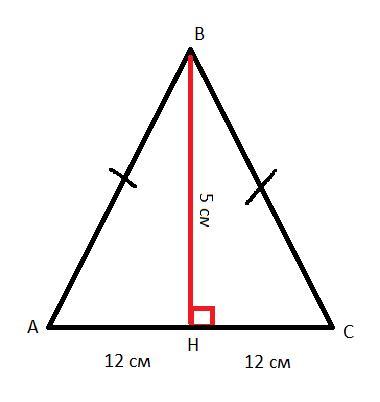
Основа рівнобедреного трикутника дорівнює 24 см, а висота, проведена до його основи, - 5 см. Знайдіть бічну сторону трикутника. У відповідь запишіть повний розв'язок задачі.
Ответы
Автор ответа:
0
Давайте вирішимо цю задачу. Оскільки це рівнобедрений трикутник, то бічні сторони будуть рівними. Позначимо одну з цих сторін як "х".
Застосуємо теорему Піфагора, використовуючи половину основи як одну зі сторін прямокутного трикутника, а висоту як іншу сторону. Отримаємо наступне рівняння:
х^2 = (24/2)^2 + 5^2
Спростимо його:
х^2 = 12^2 + 5^2
х^2 = 144 + 25
х^2 = 169
Тепер візьмемо квадратний корінь з обох боків, щоб отримати значення "х":
х = √169
х = 13
Отже, бічна сторона трикутника дорівнює 13 см.
Застосуємо теорему Піфагора, використовуючи половину основи як одну зі сторін прямокутного трикутника, а висоту як іншу сторону. Отримаємо наступне рівняння:
х^2 = (24/2)^2 + 5^2
Спростимо його:
х^2 = 12^2 + 5^2
х^2 = 144 + 25
х^2 = 169
Тепер візьмемо квадратний корінь з обох боків, щоб отримати значення "х":
х = √169
х = 13
Отже, бічна сторона трикутника дорівнює 13 см.
Автор ответа:
0
Ответ:
AB = BC = 13 см
Объяснение:
Дано: ΔABC - равнобедренный;
AC = 24 см;
BH = 5 см
Найти: AB,BC
Решение:
1) По свойствам равнобедренного треугольника, высота, проведённая к его основанию, делит его пополам, т.е. AH = HC = AC:2 = 24:2 = 12
2) Рассмотрим треугольник BHC
Т.к. BH⊥AC = > ΔBHC - прямоугольный
3) По т. Пифагора:
CH²+BH² = BC²
BC = √(5²+12²) = √(25+144) = √169 = 13
4) Т.к. ΔABC - равнобедренный ⇒ AB = BC = 13 см
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: darimixw
Предмет: Українська мова,
автор: luffy031109
Предмет: Математика,
автор: zharykdiana
Предмет: Алгебра,
автор: KoteVuchenii