Question

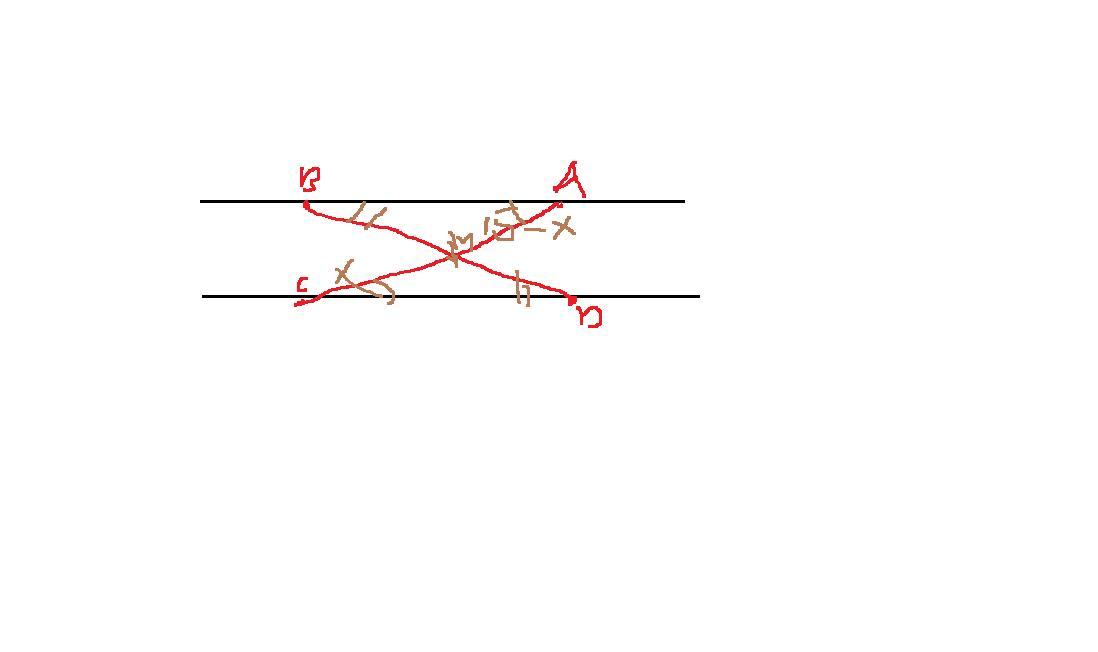
Отрезки АВ и ДС лежат на параллельных прямых, а отрезки АС и ВД пересекаются в точке М. Найдите МС, если АВ=10, ДС = 50, АС = 15

Рисунок обязательно должен быть
И все обоснования

Answer 1

Решение:

Пусть МС = х, тогда АМ = 15 - х.

Треугольник АМВ подобен треугольнику DMC, так как угол АМВ = углу DCM (как вертикальные) и угол МАВ = углу MCD (как накрест лежащие).

Соответствующие стороны треугольников пропорциональны:

АВ / DC = АМ / МС

10/50 = 15-х / х

1/5 = 15-х / х

х = 5(15-х)

х = 75 - 5х

6х = 75

х = 75:6

х = 12,5

Ответ: 12,5 см.

Answer 2

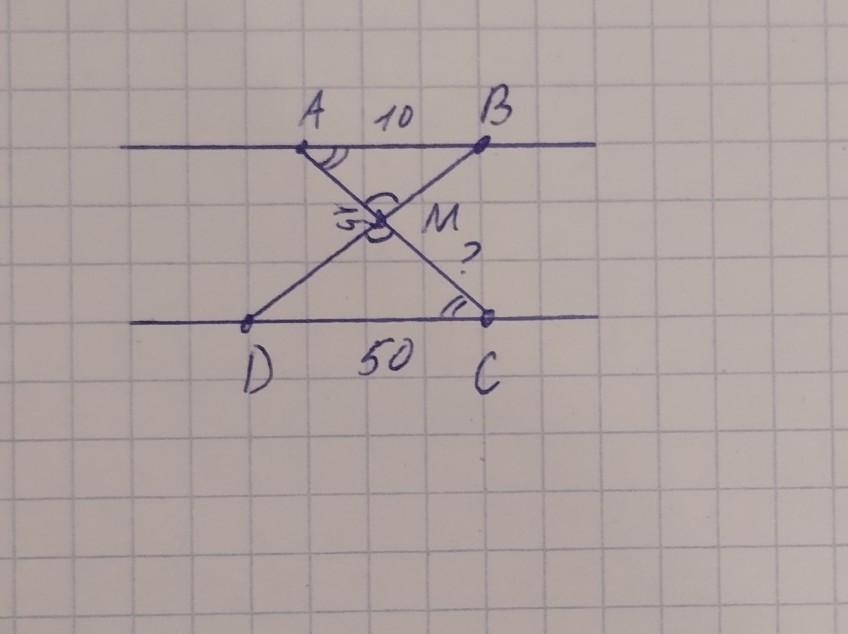
Ответ: 12,5

Объяснение: 1. треугольник CMD подобен треугольнику AMB  по 2м углам( угол DBA равен углу BDC, и угл CAB равен углу ACD как накрест лежащие при парал. прямых AB CD)

2. Из подобия следует

   CM/AM = CD/AB = K(коэф. подобия) = 5

3. Пусть СМ = х, тогда АМ = 15 - х

4. Составим пропорцию

CM/AM = 5

X / 15- х = 5( домнажаем обе части на 15 -х)

х = 5 * (15-х)

х = 75 - 5х

6х = 75

х = 75/6

х = 12,5

Поставь лайк пж, я первый раз отвечаю