Question

ооооооооооооооооооооооооооо​

Answer 1

Ответ: а) (1;0); б) √е≈1,65

Пошаговое объяснение:

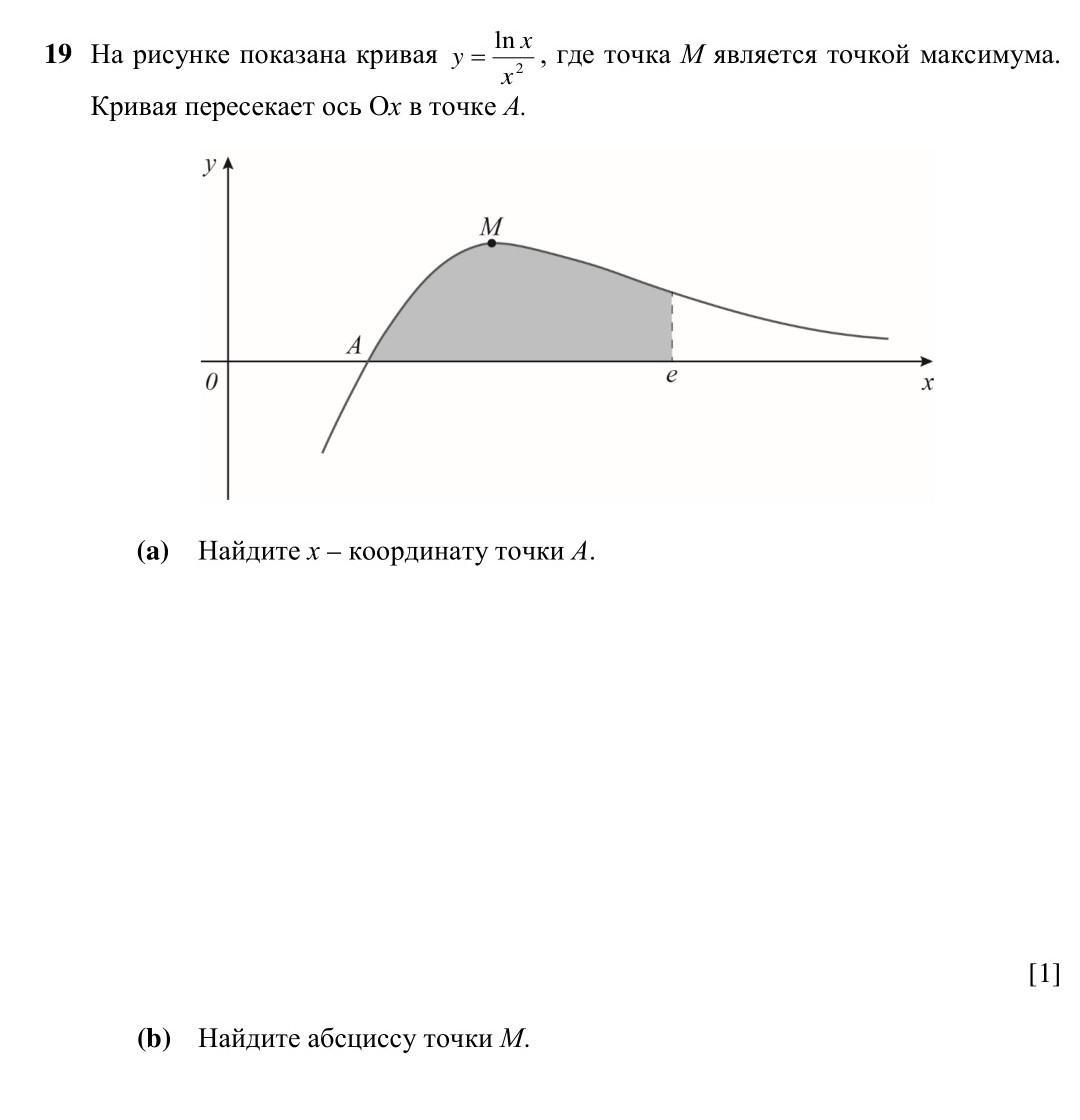
а) чтобы найти координаты точки А. найдем ln(x) / x² = 0, то есть ln x = 0

пользуясь ln(1) = 0, то x = 1

Получаем А( 1; 0)

б) точка максимума М

Находим нули функции. Для этого приравниваем производную к нулю

y' = (ln(x) / x²)

$y'=\frac{\frac{1}{x} *x^2-lnx*2x}{(x^{2}) ^{2}} =\frac{x-2xlnx}{x^4} =\frac{1-2lnx}{x^3}$

$1-2lnx=0\\lnx=2$

x = √e ≈ √2.178≈1.65

В окрестности точки x = √e (или ≈1,65) производная функции меняет знак с (+) на (-). Следовательно, точка x = 1.65 - точка максимума.

таким образом абсцисса точки М = √e ≈ 1,65