Question

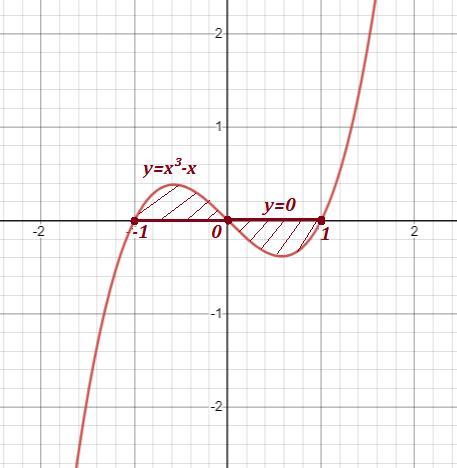
Обчисліть полощу фігури, обмежену вказаними лініями
у=х^3-х; у=0; х=-1; х=1
( с рисунком надо )

Answer 1

Ответ:   S=0,5  .  

Вычислить площадь области можно с помощью определённого интеграла .

$\bf y=x^3-x\ \ ,\ \ y=0\ \ ,\ \ x=-1\ \ ,\ \ x=1$  

Точки пересечения :    

$\bf x^3-x=0\ \ ,\ \ x(x-1)(x+1)=0\ \ ,\ \ x_1=-1\ ,\ x_2=0\ ,\ x_3=1$

Область симметрична относительно оси ОУ . Можно вычислить площадь левой половинки области, а затем удвоить результат .

$\bf \displaystyle S=\int\limit_{-1}^0\, (x^3-x)\, dx=\Big(\frac{x^4}{4}-\frac{x^2}{2}\Big)\Big|_{-1}^0=0-\Big(\frac{1}{4}-\frac{1}{2}\Big)=\frac{1}{4}=0,25$  

$\bf S_{oblasti}=2\cdot 0,25=0,5$