Алгебра. Даю 50 балів.
Виконати 1 завдання.
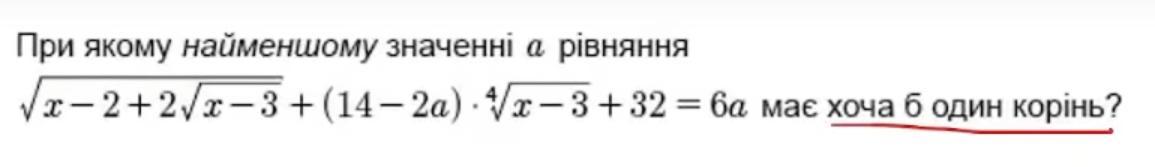
Ответы
Ответ:
а=5,5
Объяснение:
Видел данную задачу, но тот, кто задал вопрос, плохо написал условие, теперь я это узнал... Тем не менее, идея та же
Перенесу третье слагаемое вправо:
Будем рассматривать левую и правую часть как отдельные функции:
Их точка пересечения будет являться решением уравнения.
Есть два случая, при которых кординально меняется график g(x):
1)При a>7 функция бесконечно возрастает на промежутке, где она определена
2)При а<7 функция бесконечно убывает на промежутке, где она определена
Поскольку нас интересует минимальное значение параметра, мы будем рассматривать второй случай:
f(x) является бесконечно возрастающей функцией на промежутке, где она определена. Возрастающая и убывающая функция могут иметь максимум одну точку пересечения.
f(x) начинает свой путь с точки (3;33), g(x) начинает свой путь с (3;6а)
Теперь остались последние штрихи:
Если 6а>33, то графики имеют точку пересечения
Если 6а=33, то графики имеют точку пересечения в самом начале(x=3)
Если 6а<33, то графики не пересекаются
Следовательно минимально возможное значение параметра а=33/6=11/2=5,5
но.....мне, конечно, фантастика параметров интересна, но я предпочитаю лирические стихи.