имеется проволока длиной 16 м требуется оградить этой проволокой прямоугольный участок земли чтобы площадь ограждённого участка была наибольшая найдите стороны этого прямоугольного участка
Ответы
Ответ:
4 м и 4м .
Объяснение:
Имеется проволока длиной 16 м. Требуется огородить этой проволокой прямоугольный участок земли, чтобы площадь огражденного участка была наибольшей . Найти стороны этого прямоугольного участка.
Периметр прямоугольника определяется по формуле Р = 2 · ( a+ b) ,
где a- длина, b - ширина.
Если участок имеет форму прямоугольника, то длина проволоки - это периметр. Тогда сумма длины и ширина равна 8м.
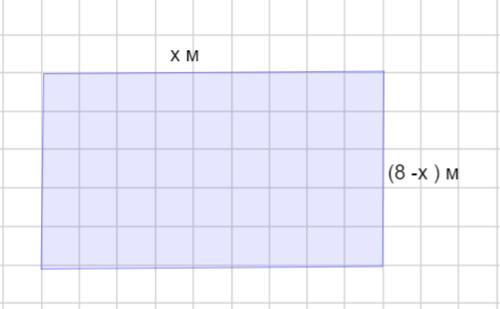
Пусть длина участка будет х м ( x>0) . Тогда ширина ( 8 - х) м ( x < 8).
Чтобы найти площадь прямоугольника, надо длину умножить на ширину.
Рассмотрим функцию
S(x) = x· (8-x) = 8x - x².
Так как полученная функция непрерывна, то найдем ее наибольшее значение на отрезке [0; 8].
Найдем производную функции S' (x) = 8 - 2x
Найдем критические точки, решив уравнение: 8-2x =0
2x =8
x = 4
Найдем значение функции на концах отрезка и в точке х= 4
S(0) = 0· (8-0) = 0
S( 4) = 4 · (8 -4) =16
S(8) = 8 · (8-0) = 0
Наибольшее значение достигается в точке х= 4
Значит, длина участка 4м , а ширина 8 - 4 =4 м.
Тогда наибольшую площадь имеет участок квадратной формы со стороной 4 м.
#SPJ1