Вища математика. Розв'язати диференційне рівняння
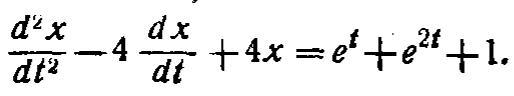
Ответы
Ответ:
Пошаговое объяснение:
Перепишу это уравнение в более привычном виде:
Это неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и со специальной правой частью.
Алгоритм решения данных уравнений предельно прост:
1. Находим общее решение соответствующего однородного уравнения.
2. Находим частное решение неоднородного уравнения.
3. Находим общее решение неоднородного уравнения, складывая общее решение однородного уравнения и частное решение неоднородного уравнения.
1. Решим соответствующее однородное уравнение:
Составляем характеристическое уравнение и находим его корни:
Получили два равных действительных корня, поэтому общее решение однородного уравнения запишется следующим образом:
2. Правую специальную часть разобьем на сумму нескольких функций:
, где
,
,
.
Теперь находим частные решения трех неоднородных уравнений ,
,
:
1) Общий вид функции имеет вид:
.
Подставляем найденные значения в соответствующее неоднородное уравнение:
Тогда частное решение первого уравнения:
2) Общий вид функции имеет вид:
.
Подставляем найденные значения в соответствующее неоднородное уравнение:
Тогда частное решение второго уравнения:
3) Общий вид функции имеет вид:
.
Подставляем найденные значения в соответствующее неоднородное уравнение:
Тогда частное решение третьего уравнения:
Теперь запишем частное решение исходного неоднородного уравнения:
3. Записываем общее решение исходного неоднородного уравнения: