Предмет: Алгебра,
автор: pomagat0r3000
довести тотожність ( вираз на фотографії)
Приложения:
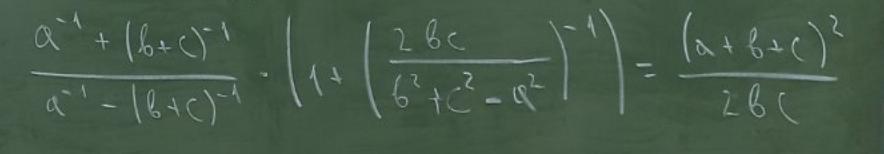
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Что и требовалось доказать
Похожие вопросы
Предмет: Другие предметы,
автор: vz09675
Предмет: Алгебра,
автор: klejnstas86
Предмет: Математика,
автор: k08620508
Предмет: Русский язык,
автор: emix65
Предмет: Русский язык,
автор: emix65