Question

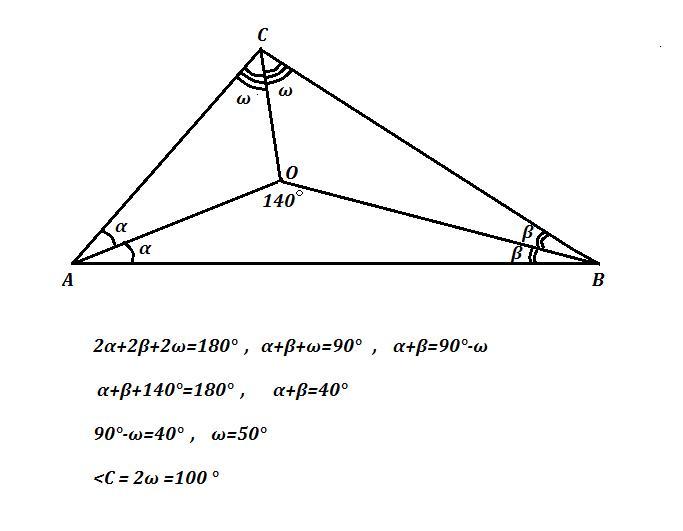
На рисунку точка O — центр вписаного кола трикутника ABC. Знайдіть кут ACB, якщо кут AOB дорівнює 140°, з поясненням, будь ласка! Даю 50 балів

Answer 1

Ответ:

∠ACB = 100°

Объяснение:

На рисунку точка O — центр вписаного кола трикутника ABC. Знайдіть кут ACB, якщо кут AOB дорівнює 140°

• Центр кола, вписаного в трикутник, є точкою перетину його бісектрис.

Розв'язання

Нехай АВС - даний трикутник. ∠AOB=140°. Знайдемо ∠ACB.

1) Так як суму кутів трикутника дорівнює 180°, то в ΔAOB:

∠ОАВ+∠ОВА=180°-∠АОВ=180°-140°=40°

2) Так як  O — центр вписаного кола трикутника ABC, то АО і ВО - бісектриси кутів САВ і СВА відповідно. Отже за означенням бісектриси кута трикутника маємо:

∠САВ=2·∠ОАВ

∠СВА=2·∠ОВА

Тоді їх сума:

$\sf \angle CAB+\angle CBA=2\cdot \angle OAB+2\cdot\angle OBA=2\cdot (\underset{40^\circ}{\underbrace{\angle OAB+\angle OBA})}=\bf 80^\circ$

3) У ΔАВС за теоремою про суму кутів трикутника знайдемо кут АСВ:

∠АСВ=180°-(∠САВ+∠СВА)=180°-80°= 100°

Відповідь: А. 100°

Answer 2

Ответ.

ΔАВС , О - центр вписанной окружности , ∠АОВ = 140° .

Центр вписанной окружности лежит на пересечении биссектрис углов .

Обозначим  ∠А=2α  ,  ∠В=2β  ,  ∠С=2ω .

Тогда ∠САО=∠ВАО=α  ,  ∠АВО=∠СВО=β  ,  ∠АСО=∠ВСО=ω  .

Сумма углов треугольника равна 180° , поэтому

∠А+∠В+∠С=2α+2β+2ω=180°   ⇒    α+β+ω=90°  ,  α+β=90°-ω  (*)

Из  ΔАОВ имеем:   ∠АОВ+α+β=180°  ,   140°+α+β=180°  ,  

α+β=180°-∠АОВ=180°-140°=40°    (**)  

Приравняем правые части равенств (*)  и  (**) .        

90°-ω=40°

90°-40°=ω

ω=50°

2ω=100°

∠АСВ=100°