Question

МЕГА СРОЧНО!!!!
Дві сторони трикутника дорівнюють 16 см і 6 см, а відношення радіуса кола, описаного навколо трикутника, до третьої стоони дорівнює 1 : 3. Знайдіть третю сторону трикутника​

Answer 1

Ответ:

Задача має два розв'язки:

1) якщо трикутник гострокутний, то третя сторона дорівнює 14 см

2) якщо тупокутний, то 2√97 см, або приблизно 19,7 см

Объяснение:

Уточнена умова:

Дві сторони трикутника дорівнюють 16 см і 6 см, а відношення радіуса кола, описаного навколо трикутника, до третьої стоони дорівнює 1 : √3. Знайдіть третю сторону трикутника​.

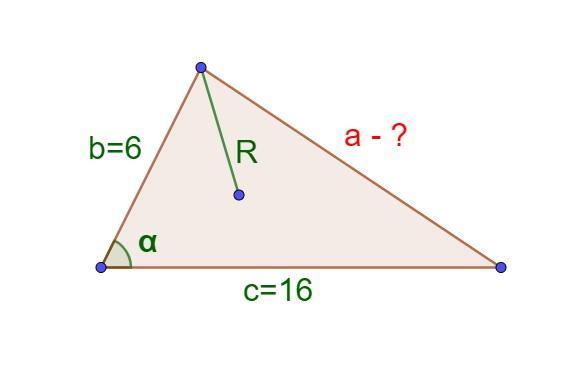
Нехай дан трикутник, сторони якого: b=6 см, с=16 см, R : a = 1 : √3.

1) За узагальненою теоремою синусів маємо:

$\dfrac{a}{sin\alpha } =2R$

де R - радіус кола, описаного навколо трикутника, а - третя сторона трикутника.

За умовою:

$\dfrac{R}{a} =\dfrac{1}{\sqrt{3} }$

a= R√3, тоді:

$sin\alpha =\dfrac{a}{2R} =\dfrac{R\sqrt{3} }{2R} =\dfrac{\sqrt{3} }{2}$

Отже, якщо:

• трикутник гострокутний, то α=60°
• якщо тупокутний, то α=120°

2) α=60°

cos 60° = 1/2

За теоремою косинусів:

а²=b²+c²-2bc•cosα

a²=6²+16²- 2 · 6 · 16 · 1/2 = 36+256-96=196

a = 14 cм

3) α=120°

cos 120° = - 1/2

а²=b²+c²-2bc•cosα

a²=6²+16²- 2 · 6 · 16 · (- 1/2) = 36+256+96=388

а = 2√97 см

Відповідь: задача має два розв'язки: 14 см або 2√97 см

#SPJ1