Question

Відстань між центрами двох кіл, що дотикаються, дорівнює 15 см. Знайдіть радіуси цих кіл, якщо один з них у чотири рази більший за інший. Розгляньте всі можливі випадки

Answer 1

Відповідь:

1) R1 = 12 см.; R2 = 3 см.

2) R1 = 20 см.; R2 = 5 см.

Пояснення:

Якщо радіус більшого з кіл у чотири рази більший за радіус меньшого, то:

R1 / R2 = 4 / 1

Маємо:

R1 = 4R2 ( 1 )

Два кола, що дотикаються можуть бути розміщені одне відносно другого у двох випадках.

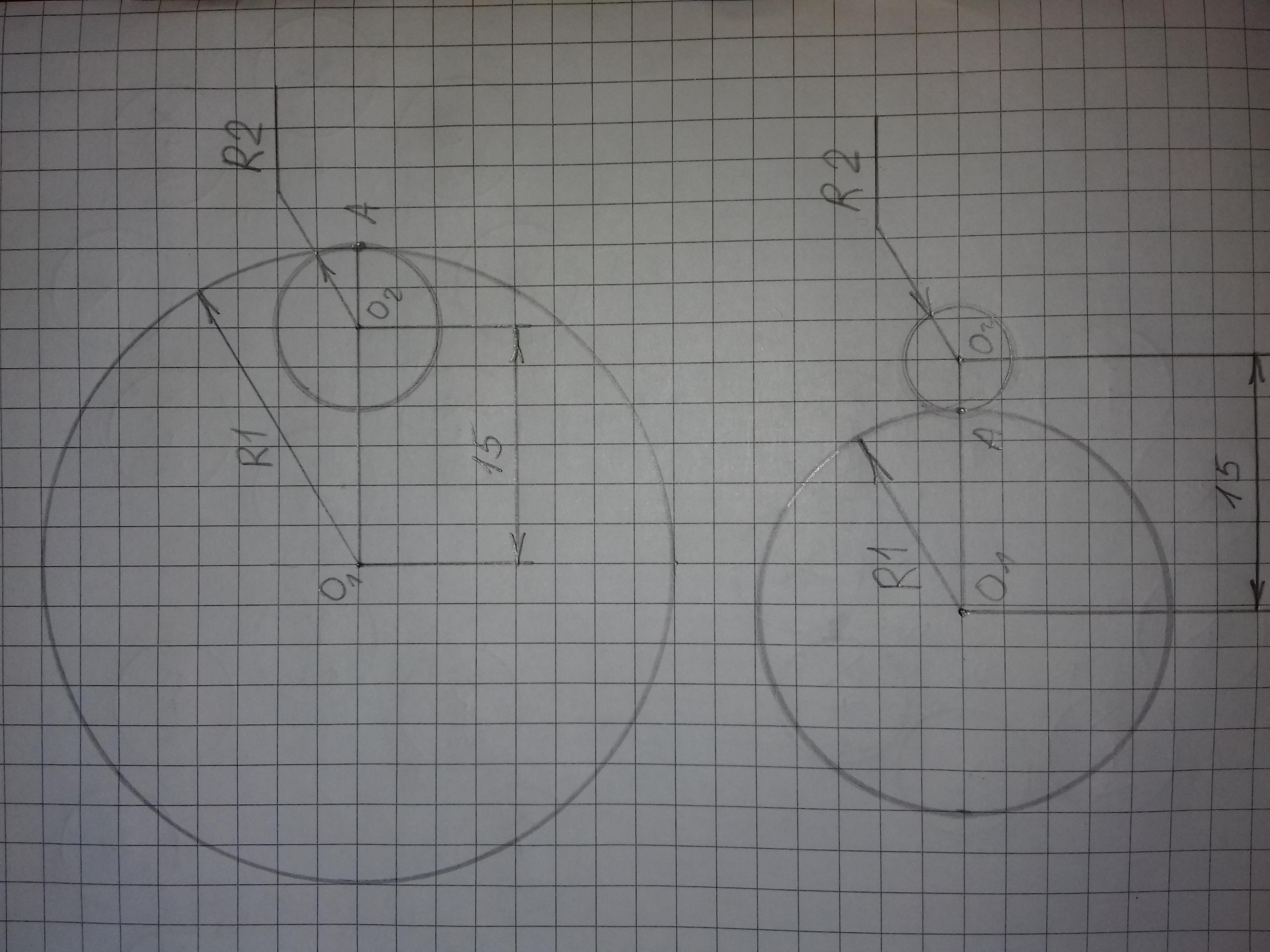
1 випадок. Меньше коло знаходиться в середині більшого. У такому випадку точка дотикання ( А ) знаходиться по один бік від центрів обох кіл ( О1 та О2 ).

Оскільки відстань між центрами двох кіл дорівнює 15 см., маємо:

R1 + R2 = 15 ( 2 )

Підставимо рівняння ( 1 ) до рівняння ( 2 ):

4R2 + R2 = 15

5R2 = 15

R2 = 15 / 5

R2 = 3 см.

Підставимо знайдене значення R2 до рівняння ( 2 ):

R1 + 3 = 15

R1 = 15 - 3

R1 = 12 см.

2 випадок. Меньше коло знаходиться назовні від більшого. У такому випадку точка дотикання ( А ) знаходиться між центрами обох кіл ( О1 та О2 ).

Оскільки відстань між центрами двох кіл дорівнює 15 см., маємо:

R1 - R2 = 15 ( 3 )

Підставимо рівняння ( 1 ) до рівняння ( 3 ):

4R2 - R2 = 15

3R2 = 15

R2 = 15 / 3

R2 = 5 см.

Підставимо знайдене значення R2 до рівняння ( 3 ):

R1 - 5 = 15

R1 = 15 + 5

R1 = 20 см.