Срочно!!! Питання №24 Побудуйте графік функції у = x2 + 4x + 3. Користуючись графіком, знайдіть: 1. область значень функції ------[ _ ; + ∞ ) 2. проміжки зростання функції [; +∞) 3. та спадання функції (-∞;)
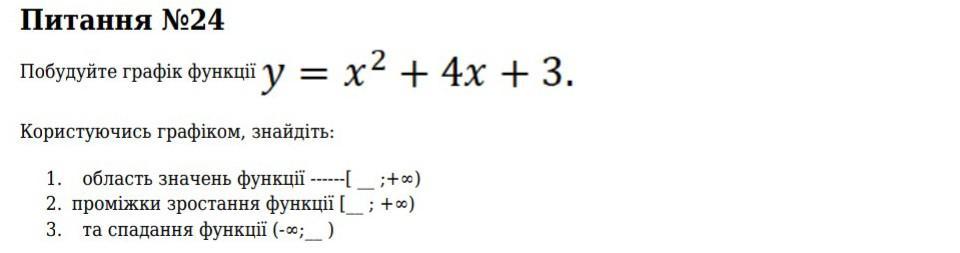
Ответы
Ответ:
Для побудови графіка функції y=x^2+4x+3 треба скористатися методом допоміжних прямих та знайти вершину параболи і перетин з осі Оу.
y=x^2+4x+3 можна переписати у такому вигляді:
y = (x+2)^2 - 1
Отже, вершина параболи знаходиться у точці (-2, -1). Це дає нам інформацію про те, що графік функції є параболою, що відкривається догори.
Також, функція y=x^2+4x+3 перетинає осі координат в точках (-3, 0) та (-1, 0).
Отже, графік функції має вигляд:
```
|
3| x
| x x
2| x x x
| x x x x
1| x x x x x
| x x x x x x
0|______________________
-3 -2 -1 0
```
1. Область значень функції: оскільки парабола відкривається догори, то мінімальне значення функції -1 (в точці (-2, -1)). Отже, область значень функції - від -1 до +безмежності.
2. Проміжки зростання функції: функція зростає на відрізку (-безмежність, -2) і на відрізку (-1, +безмежність).
3. Проміжки спадання функції: функція спадає на відрізку (-2, -1).