Предмет: Геометрия,
автор: lerkakakaska828
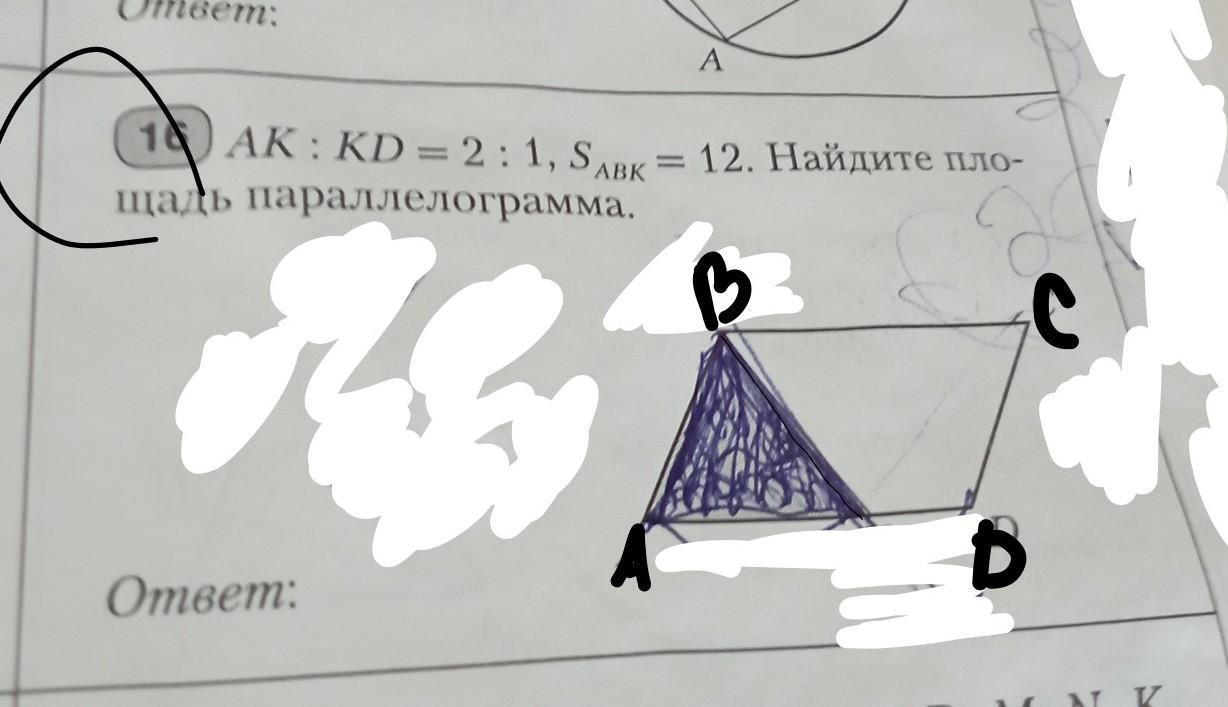
AK:KD=2:1, Sabk = 12. Найдите площадь параллелограмма
Приложения:
Ответы
Автор ответа:
1
Ответ:
Площадь параллелограмма равна 36 ед².
Объяснение:
AK:KD=2:1, Sabk = 12. Найдите площадь параллелограмма.
- Площадь треугольника равна половине произведения двух его сторон на синус угла между ними
S= ½ • AB • AD • sin α
- Площадь параллелограмма равна произведению двух сторон на синус угла между ними.
S = AB • AD • sin α
Решение
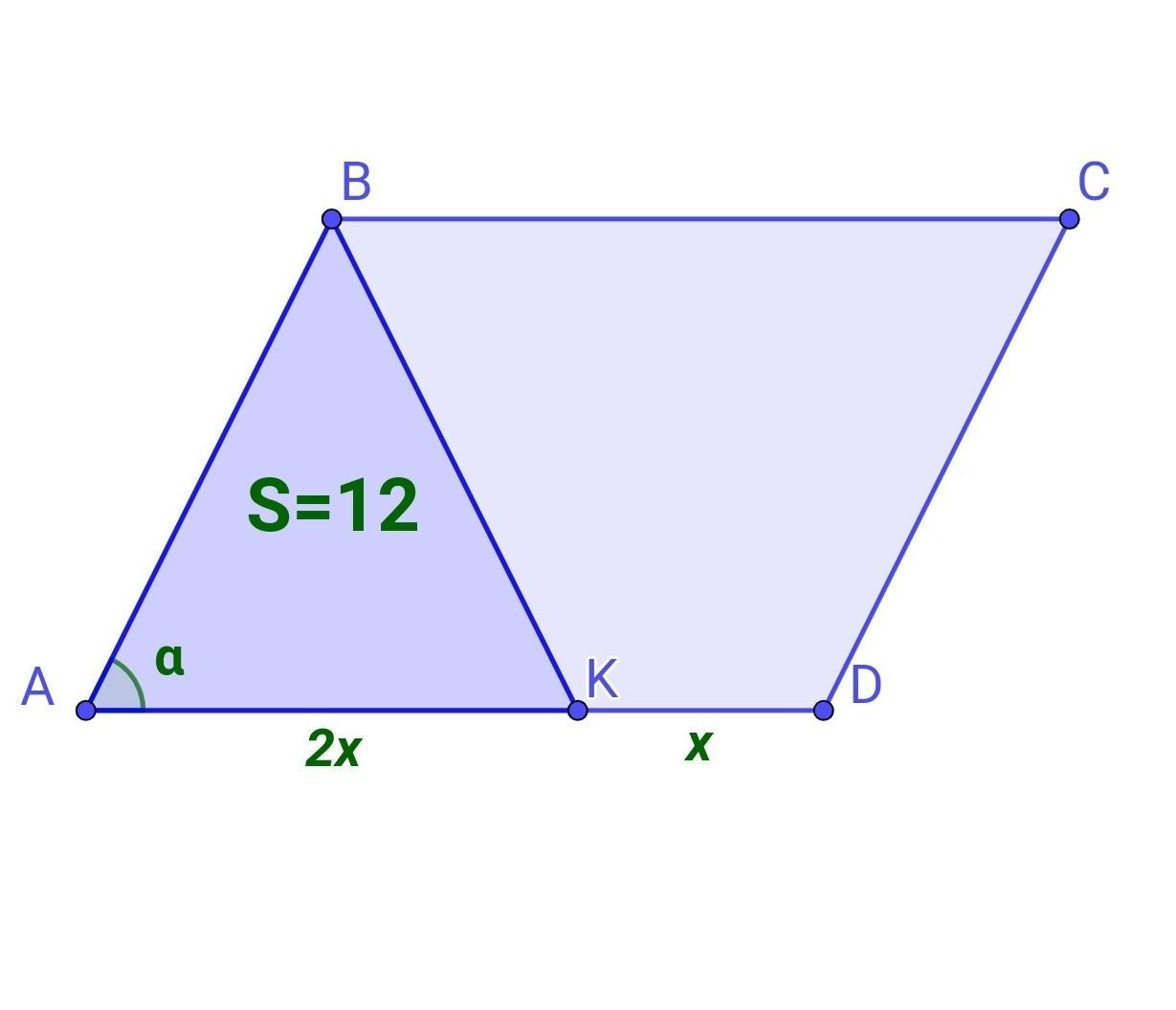
Пусть АК = 2х, KD = x, где х - коэффициент пропорциональности.
Тогда сторона AD (согласно аксиоме измерения отрезков):
AD = AK + KD = 2x + x = 3x.
Площадь треугольника АВК:
S(ABK) = ½ • AB • 2x • sinα = AB • x • sin α, откуда выразим сторону АВ:
Площадь параллелограмма ABCD:
S(ABCD) = AB • AD • sin α
Подставим найденное значение АВ:
Таким образом, площадь параллелограмма ABCD равна 36 кв.ед.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Литература,
автор: nesterovakira728
Предмет: Алгебра,
автор: m7362108
Предмет: Алгебра,
автор: StarSpangledBanner
Предмет: История,
автор: kolyalalja333
Предмет: Английский язык,
автор: MedicusBear