Предмет: Алгебра,
автор: elmirpochta
УМАЛЯЮ СРОЧНО ДАМ 100 БАЛОВ ВСЕ ЧТО УГОДНО
Приложения:
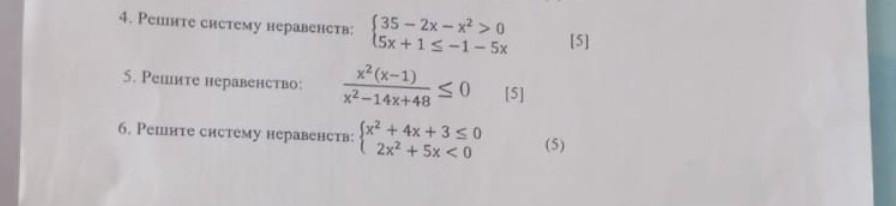
Ответы
Автор ответа:
1
4.
5.
6.
elmirpochta:
жаль что поздно все равно спасибо
Похожие вопросы
Предмет: Українська мова,
автор: oksencukolga5
Предмет: Алгебра,
автор: kamereraleksandra
Предмет: Математика,
автор: 08877
Предмет: Физика,
автор: naaaastyaaaaaaaa