Предмет: Геометрия,
автор: romankot1313
Три кола зовнішньо попарно дотикаються одне до одного. Відстані між їхніми центрами дорівнюють 6 см, 7 см і 9 см. Визначте радіуси цих кіл.
Для 7 классу, без теореми Піфагора.
Ответы
Автор ответа:
3
Ответ:
Радиусы окружностей равны 2 см, 4 см, 5 см.
Объяснение:
Три окружности внешне попарно касаются друг с другом. Расстояния между их центрами равны 6 см, 7 см и 9 см. Определите радиусы этих кругов.
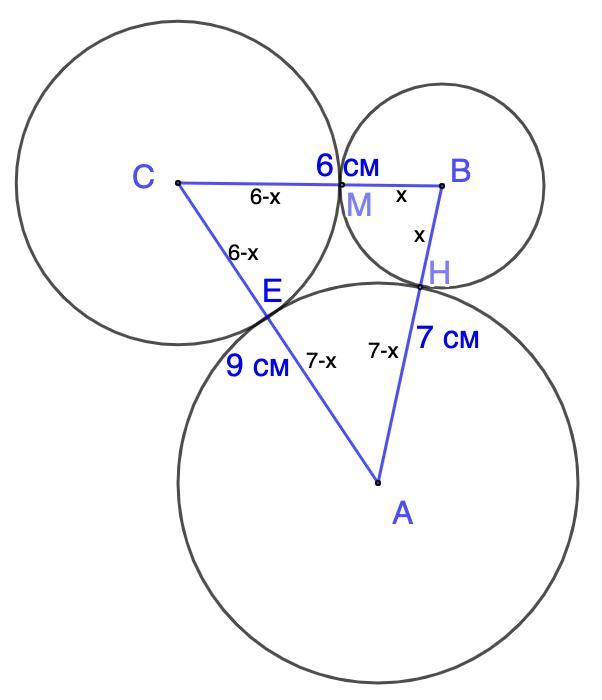
Дано: Окр.С; Окр.В; Окр.А - попарно внешне касаются друг друга.
СВ = 6 см; АВ = 7 см; АС = 9 см.
Найти: радиусы окружностей.
Решение:
- Центры касающихся окружностей и точка их касания лежат на одной прямой.
⇒ СЕ и СМ - радиусы Окр.С;
ВМ и ВН - радиусы Окр.В;
АН и АЕ - радиусы Окр.А.
Пусть ВМ = ВН = х см.
Тогда АН = АЕ = 7 - х (см); СМ = СЕ = 6 - х (см).
АС = АЕ + СЕ = 9 см
7 - х + 6 - х = 9
- 2х = -4 |:(-2)
x = 2
⇒ ВМ = ВН = 2 см
АН = АЕ = 7 - 2 = 5 (см)
СМ = СЕ = 6 - х = 6 - 2 = 4 (см)
Радиусы окружностей равны 2 см, 4 см, 5 см.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: bakhrim45
Предмет: Математика,
автор: RabbitPik
Предмет: Қазақ тiлi,
автор: ktanjiro228109
Предмет: Математика,
автор: VASKA57
Предмет: Физика,
автор: karimalkam111