Предмет: Алгебра,
автор: govnoblytyou
50 БАЛЛОВ, СРОЧНО
РЕШИТЕ СИСТЕМУ НЕРАВЕНСТВ:
Приложения:
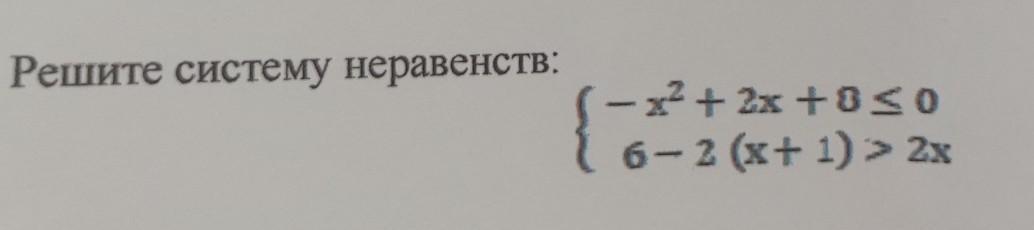
Ответы
Автор ответа:
1
Ответ:
Система неравенств .
Сначала преобразуем неравенства и разложим на множители .
Пересечением множеств, а значит и решением системы неравенств является множество .
Ответ: .
Приложения:


Похожие вопросы
Предмет: Геометрия,
автор: aiganymbeisenbek
Предмет: Русский язык,
автор: juliasuprun312
Предмет: Математика,
автор: vikysi4kaa03
Предмет: Математика,
автор: nvmediapr
Предмет: Математика,
автор: MayuraGrey