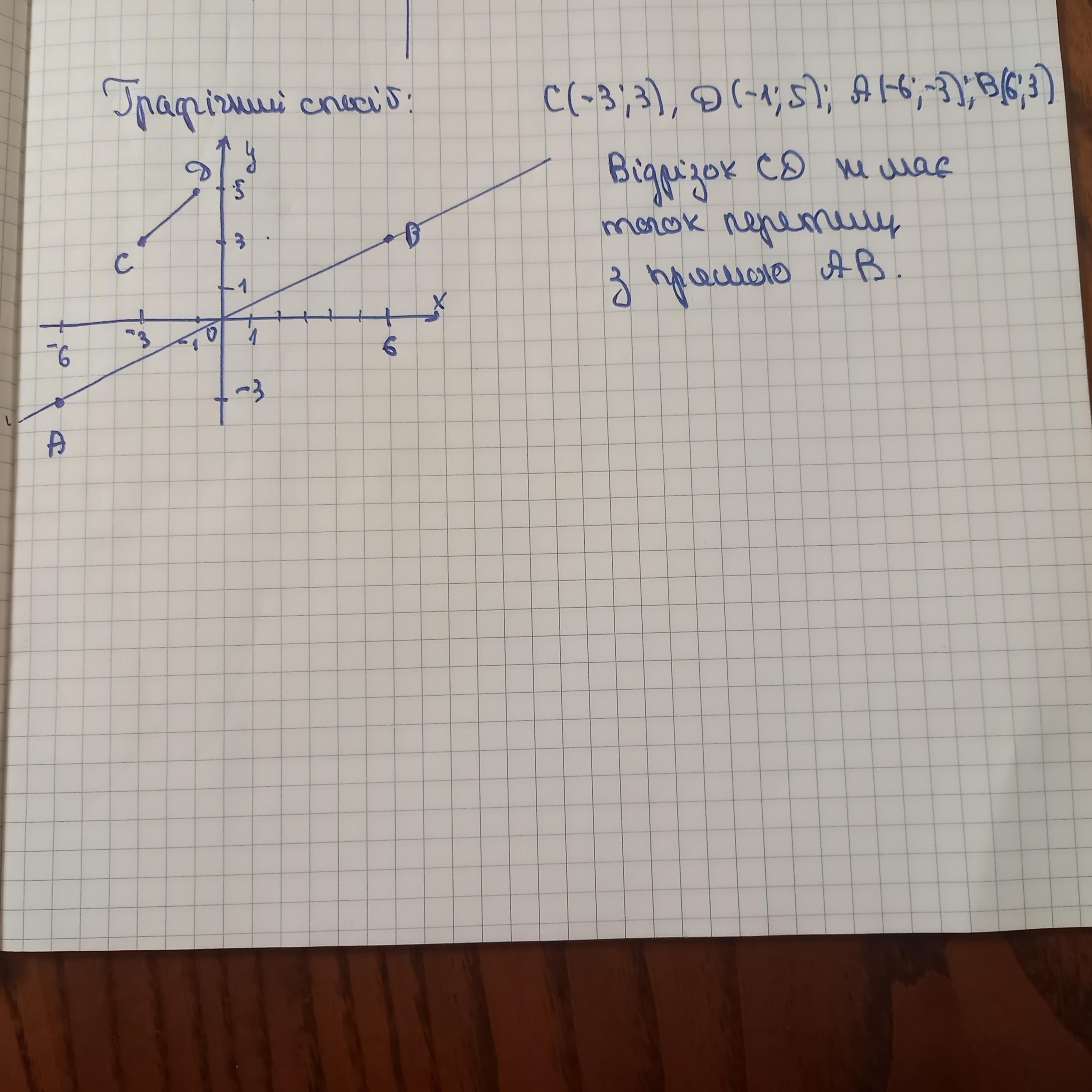
В координатній площині побудували відрізок CD кінцями якого є точки С ( -3; 3) і D ( - 1; 5 ) та пряму АВ яка проходить через точки А ( -6; -3 ) і В ( 6; 3) знайти координати точки перетину відрізка CD і прямої АВ.
Ответы
Відповідь:
Для знаходження точки перетину відрізка CD і прямої АВ, спочатку знайдемо рівняння прямої АВ за допомогою формули визначення коефіцієнта наклона:
k = (y2 - y1) / (x2 - x1)
де (x1, y1) і (x2, y2) - координати точок А і В.
Підставимо дані:
k = (3 - (-3)) / (6 - (-6))
= 6 / 12
= 1/2
Тепер, використовуючи рівняння прямої, знайдемо рівняння прямої АВ:
y - y1 = k(x - x1)
Замінимо (x1, y1) = (-6, -3):
y - (-3) = (1/2)(x - (-6))
y + 3 = (1/2)(x + 6)
2y + 6 = x + 6
x - 2y = 0
Тепер ми маємо рівняння прямої АВ. Далі, знайдемо точку перетину з відрізком CD. Для цього підставимо координати точок C і D в рівняння прямої:
Для точки C (x, y) = (-3, 3):
x - 2y = 0
-3 - 2(3) = 0
-3 - 6 = 0
-9 = 0 (невірно)
Для точки D (x, y) = (-1, 5):
x - 2y = 0
-1 - 2(5) = 0
-1 - 10 = 0
-11 = 0 (невірно)
Отже, відрізок CD і пряма АВ не перетинаються в одній точці на площині. Можливо, у вихідних даних або обчисленнях допущена помилка. Будь ласка, перевірте дані і обчислення і повторіть розрахунки.
Відповідь: відрізок СD та пряма АВ не перетинаються.
Покрокове пояснення:
розв'язання завдання додаю